Vettori vs quaternioni – Algebra geometrica

Quando abbiamo trattato dell’algebra geometrica 2D, abbiamo capito che i bivettori sono in grado di ruotare i vettori. Siamo curiosi di verificare se la cosa funziona anche in 3D.

Calcoliamo il prodotto tra un vettore ed un bivettore: il vettore si può scomporre in una componente nel piano del bivettore $a_\parallel$ ed una perpendicolare ad esso. Dato che non possiede una forma, possiamo rimodellare il bivettore in modo che risulti $F = (a_\parallel \wedge c)$

Prodotto tra un vettore ed un bivettore in 3D

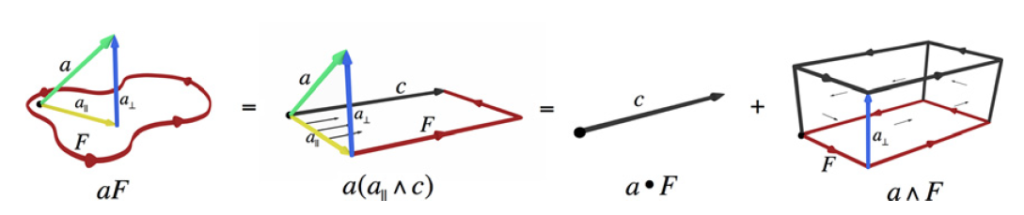
Il risultato del prodotto sarà composto da due parti: $a_\parallel F + a_\perp F = |a_\parallel||c| + a_\perp \wedge F$ ovvero il vettore $a_\parallel$ ruotato di $\pi/2$ nel piano di F ed il trivettore $a \wedge F$ .
Quindi effettivamente il bivettore ha ruotato la componente del vettore che giaceva nel suo piano, ma ha anche generato un volume che, per la rotazione che andiamo cercando, rimane … indigesto.
Se proviamo a scambiare i fattori, la rotazione di $a_\parallel$ si inverte, ma il volume rimane identico.

Senza farci venire ulteriori mal di testa, la soluzione è già stata enunciata quando abbiamo parlato di rotori: il prodotto a sandwich $BvB^{-1}$ è quel che ci vuole per generare una rotazione pura e far sparire il trivettore.

$v = v_1 e_1 + v_2 e_2 + v_3 e_3$
$B = w + x e_1e_2 + y e_2e_3 + z e_3e_1$
$B^\dagger = w - x e_1e_2 - y e_2e_3 - z e_3e_1$
con $w^2 + x^2 + y^2 + z^2 = 1$ perché

$v' = BvB^\dagger$ ruotato nel piano di $B$ di $2 \theta$

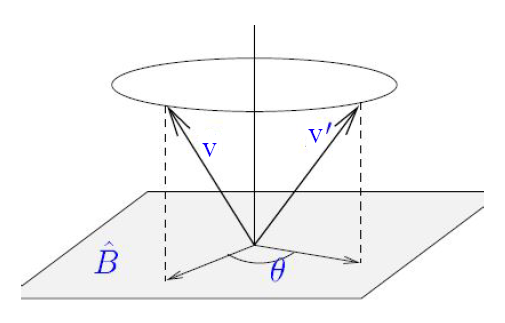
e dopo lunghi e noiosissimi calcoli, otterremo la matrice di rotazione dei quaternioni:

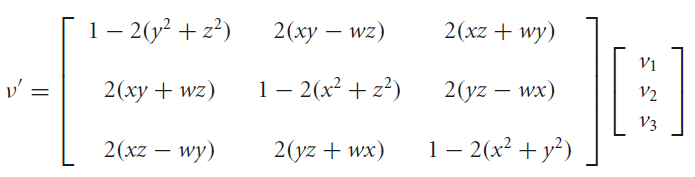
che dimenticheremo molto volentieri, affidandoci totalmente alla potenza del prodotto a sandwich!

Le rotazioni in 3D NON sono commutative e questo è un importante elemento a favore dell’utilizzo dell’AG, la quale porta la non-commutatività nel suo DNA.
Per calcolare due rotazioni successive, dunque procederemo in questo modo:

$v' = BvB^\dagger = exp(-i_1\theta_1/2) \: v \: exp(i_1\theta_1/2)$

rappresenta la prima rotazione e la seconda agirà sul risultato della prima, ovvero:

$v' = CBvB^\dagger C^\dagger = exp(-i_2\theta_2/2)\: exp(-i_1\theta_1/2)\: v \: exp(i_1\theta_1/2)\: exp(i_2\theta_2/2)$

in 3D (e soltanto in 3D) possiamo identificare un’unica rotazione come risultante delle due sopramenzionate:

$\begin{equation} exp(e_1e_2\: \frac{\pi}{4}) \: exp(e_2e_3\: \frac{\pi}{4}) = [\cos \frac{\pi}{4} + e_1e_2 \sin \frac{\pi}{4}][\cos \frac{\pi}{4} + e_2e_3 \sin \frac{\pi}{4}]$
$\begin{equation} = \frac{1}{2} (1 + e_1e_2)(1 + e_2e_3) = \frac{1}{2} + \frac{e_1e_2 + e_2e_3 + e_1e_3}{\sqrt 3} \frac{\sqrt 3}{2}$
$\begin{equation} = \cos \frac{\pi}{3} + \frac{e_1e_2 + e_2e_3 + e_1e_3}{\sqrt 3} \: \sin \frac{\pi}{3}$
$\begin{equation} = exp \left( \frac{e_1e_2 + e_2e_3 + e_1e_3}{\sqrt 3} \: \frac{\pi}{3} \right)$

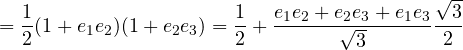
che infine corrisponde ad una rotazione di 120 gradi su un piano che facciamo fatica ad identificare: per la nostra immaginazione è molto più facile visualizzare l’asse di rotazione.
Per trovarlo ricorriamo alla nota dualità: $(e_1e_2 + e_2e_3 + e_1e_3)(e_3e_2e_1) = e_1 - e_2 + e_3$