Hamilton voleva estendere i numeri complessi espressi come ![]() e rappresentati nel piano di Argand-Gauss allo spazio tridimensionale, ma non ci riuscì. Propose quindi un oggetto quadridimensionale della forma
e rappresentati nel piano di Argand-Gauss allo spazio tridimensionale, ma non ci riuscì. Propose quindi un oggetto quadridimensionale della forma ![]() dove
dove ![]() ,
, ![]() e
e ![]() sono simboli che si comportano come l’unità immaginaria
sono simboli che si comportano come l’unità immaginaria ![]() . Per la verità, siccome i quaternioni sono normalizzati a 1, non abbiamo quattro parametri indipendenti, ma solo tre, quindi si tratta a tutti gli effetti di un oggetto 3D.
. Per la verità, siccome i quaternioni sono normalizzati a 1, non abbiamo quattro parametri indipendenti, ma solo tre, quindi si tratta a tutti gli effetti di un oggetto 3D.
La proprietà fondamentale dei quaternioni venne in mente ad Hamilton in un lampo di genio durante una passeggiata e fu talmente importante da essere scolpita su una targa in pietra posta sul Broom bridge presso Dublino: ![]()

L’importanza dei quaternioni è legata al fatto che riescono a rappresentare le rotazioni nello spazio tridimensionale, volgendo un apparente problema (la non commutatività) in una spettacolare dimostrazione di correttezza, perché anche le rotazioni 3D non sono commutative.
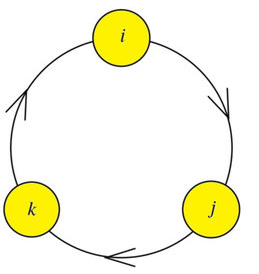
Osserviamo che le relazioni tra le basi dei quaternioni e le basi dei bivettori sono perfettamente sovrapponibili, a patto che li mettiamo in relazione come segue:
| convenzione più diffusa (un cambiamento di segno) | convenzione alternativa (tre cambiamenti di segno) |
il segno meno deriva dal fatto che Hamilton concepiva le basi come un sistema sinistrorso, mentre il sistema attualmente in uso è destrorso (angoli positivi in senso antiorario). Per questo motivo una delle basi deve cambiare segno (o tre).
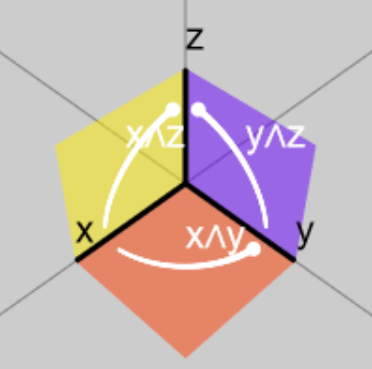
Il successo dei quaternioni portò Hamilton ad azzardare l’identificazione delle tre basi i, j e k con le tre basi dello spazio vettoriale 3D: li chiamava quaternioni puri, quelli cioè senza parte scalare. Anzi, fu lui a coniare l’espressione vettore e ancora oggi i simboli i, j e k sono usati per indicare i versori dello spazio 3D.
Tuttavia – come abbiamo detto in apertura – Maxwell notò che l’energia cinetica espressa per mezzo dei quaternioni intesi come vettori risultava negativa: il che era inaccettabile.
Qualche anno dopo, anche Minkowski si trovò a dover esprimere lo spaziotempo di Einstein a quattro dimensioni, ma anziché utilizzare i quaternioni, preferì il formalismo vettoriale di Gibbs e Heaviside. I quaternioni, dunque finirono presto nel dimenticatoio e furono riscoperti solo con l’avvento della computer graphics e della necessità di modellare al calcolatore le rotazioni 3D.
Oggi possiamo finalmente capire l’incredibile equivoco che si generò: le tre basi dei quaternioni sono da intendersi come bivettori e quindi è chiaro che riescono a modellare le rotazioni, ma non vanno considerati come spazio vettoriale! In un certo senso … avevano tutti ragione.
Questi due mondi si trovano riuniti nelle otto dimensioni dell’algebra geometrica 3D.
Potremmo proseguire con lo studio dei quaternioni, ma non lo facciamo perché l’algebra geometrica – ancora una volta – riesce ad includere e illuminare anche questo argomento, rendendolo comprensibile.
Parleremo allora di rotori 3D, dei quali possiamo dire che i quaternioni sono la forma … offuscata (si veda l’ottima pagina di Marc Ten Bosch Let’s remove quaternions from every 3D engine).
