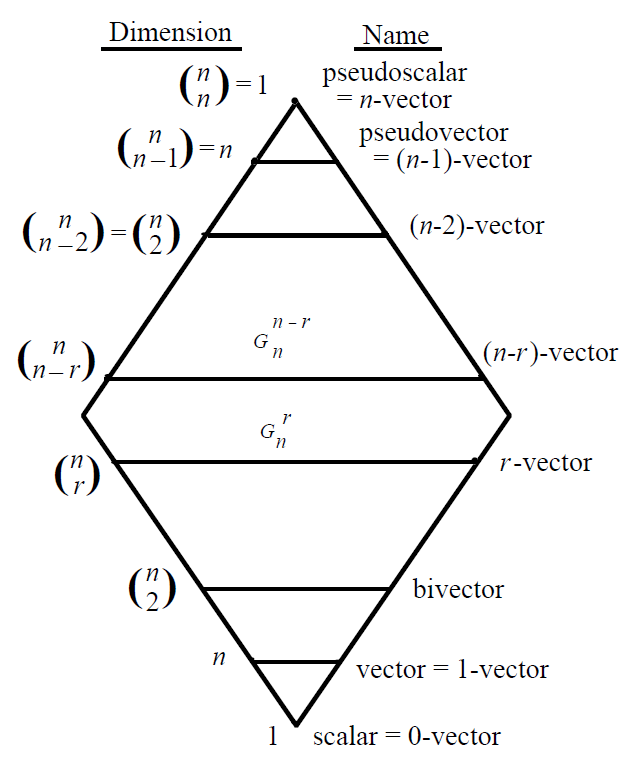
Lo pseudoscalare – Algebra geometrica

Il numero delle basi dei vari elementi di un’algebra geometrica di dimensione $n$ si ricava dalla riga $n+1$ del triangolo di Pascal. Questa struttura è simmetrica e quindi, così come vi è solo un tipo di scalare, avremo una sola base per l’elemento di grado massimo che prenderà il nome di pseudoscalare, indipendentemente dalla dimensione $n$ .

– in 1D lo pseudoscalare è semplicemente $e_1$
– in 2D lo pseudoscalare è $e_1e_2$ (= $- e_2e_1$ )
– in 3D lo pseudoscalare è $e_1e_2e_3$ (= $- e_3e_2e_1$ )
– in 4D lo pseudoscalare è $e_1e_2e_3e_4$ (= $e_4e_3e_2e_1$ )

Abbiamo visto che sia in 2D che in 3D lo pseudoscalare al quadrato vale -1, ma non si tratta di una regola generale: per algebre a segnatura uniforme abbiamo la seguente sequenza

dimensione	1	2	3	4	5	6	7	8 …
segno di $I^2$	+	–	–	+	+	–	–	+

Lo pseudoscalare in 2D anticommuta con i vettori ed infatti per questo motivo non lo identifichiamo con l’unità immaginaria $i$ . In 3D, invece, verifichiamo che non solo commuta con i vettori ma con tutti gli elementi. Insomma, la proprietà di commutazione dello pseudoscalare dipende sia dalla dimensione dello spazio che dal grado dell’elemento, secondo la seguente tabella:

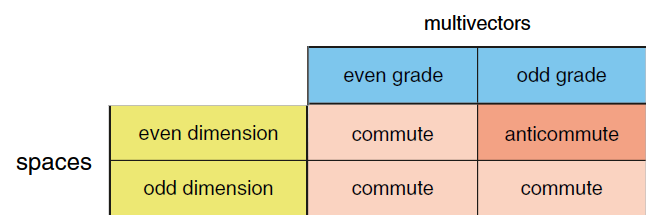
Il nome pseudoscalare deriva dal fatto che si comporta come uno scalare, cioè è immune alle rotazioni ma subisce la trasformazione di parità (l’inversione di tutti gli assi spaziali). In 2D e 3D si trasforma nel suo negativo.

Ricordiamo alcune importanti proprietà dello pseudoscalare $I$ di $\mathbb{G}^3$ :
$I^2 = -1$
$I^\dagger = -I$
$IM = MI$ per ogni multivettore in $\mathbb{G}^3$
$\begin{equation} I^{-1} = \frac{I^\dagger}{|I^2|} = -I$

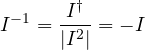
In generale, in uno spazio a $n$ dimensioni, se $I^{-1} = I^\dagger$ allora $I^{-1} = (-1)^{\frac{n(n-1)}{2}}I$
quindi abbiamo visto che in 2D e 3D $I^{-1} = -I$ e poi la sequenza dei segni per dimensioni superiori procede alternandosi a coppie: $+ + - - + + …$