Abbiamo detto che il multivettore M è la combinazione lineare di elementi di grado diverso:![]()
Queste quattro componenti si distinguono grazie al loro comportamento rispetto alle trasformazioni di base: rotazione ed inversione degli assi.
La rotazione è in grado di modificare vettori e bivettori, ma lascia invariati scalari e pseudoscalari.
L’inversione degli assi, invece, è in grado di cambiare i vettori e, dato che modifica il segno dello pseudoscalare, commuta la terna destrorsa in sinistrorsa, lasciando invariati gli scalari ed i bivettori.
Grazie a queste proprietà, possiamo costruire la seguente tabella (considerando lo spazio 3D):
| Scalare | Vettore | Bivettore | Pseudoscalare | |
|---|---|---|---|---|
| Inversione | – | si | – | si |
| Rotazione | – | si | si | – |
| Grandezze fisiche | energia, massa, lunghezza, tempo, densità, potenziale elettrico | spostamento, velocità, accelerazione, campo elettrico | velocità angolare, accelerazione angolare, momento angolare, campo magnetico, dipolo magnetico, | flusso magnetico, elicità |
E’ interessante osservare da vicino il componente probabilmente più elusivo: lo pseudoscalare. Ora finalmente ha un “abito” fisicamente esplorabile. Il flusso magnetico è il prodotto tra il bivettore campo B ed il vettore direzione; l’elicità è la proiezione del bivettore rotazione nella direzione della quantità di moto.
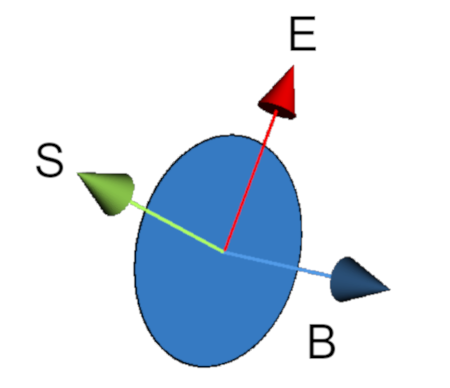
E’ interessante notare che il vettore di Poynting, nonostante nasca da un prodotto vettoriale, NON è un bivettore. Questo perché uno dei due fattori del prodotto vettoriale in realtà è un bivettore. E siccome E e B (intesi come vettori) sono perpendicolari, allora E si trova nel piano di B e dunque il prodotto esterno ![]() avrà natura vettoriale e sarà perpendicolare ad E.
avrà natura vettoriale e sarà perpendicolare ad E.
![]()
Allo stesso modo, la forza di Lorenz è un vettore, nonostante scaturisca da un prodotto vettoriale: ![]()
infatti, dato che ![]() e B (intesi come vettori) sono perpendicolari, allora
e B (intesi come vettori) sono perpendicolari, allora ![]() si trova nel piano di B e dunque il prodotto esterno
si trova nel piano di B e dunque il prodotto esterno ![]() avrà natura vettoriale e sarà perpendicolare a
avrà natura vettoriale e sarà perpendicolare a ![]() .
.
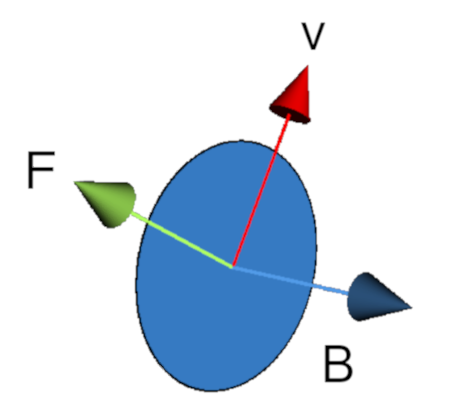
L’AG chiarisce anche un aspetto oscuro della forza di Lorenz: perché si manifesta perpendicolarmente alla velocità? Nella situazione analoga relativa al campo elettrico, la particella carica sente una forza diretta lungo le linee del campo elettrico, invece nel caso del campo magnetico, sente una forza perpendicolare. La risposta sta, ancora una volta, nel fatto che il bivettore B è una grandezza planare dotata di un verso di rotazione, non una freccetta come un vettore. Ecco perché la particella sente una forza che ne incurva la traiettoria.
