In 3D aggiungiamo la nuova base ![]() e quindi se valutiamo tutte le combinazioni come già fatto nel caso 2D, otterremo:
e quindi se valutiamo tutte le combinazioni come già fatto nel caso 2D, otterremo:
![]()
In tre dimensioni quindi l’algebra geometrica è generata da 8 basi:

Non sarà sfuggito che per ogni dimensione aggiuntiva si raddoppiano le basi e la loro distribuzione per grado segue la riga ![]() del triangolo di Pascal.
del triangolo di Pascal.
Rispetto al mondo 2D ora abbiamo altri due bivettori base e tutti e tre hanno la proprietà notevole:
![]()
ma anche il trivettore: ![]() quindi possiamo dire che bivettori e trivettori sono isomorfi all’unità immaginaria
quindi possiamo dire che bivettori e trivettori sono isomorfi all’unità immaginaria ![]() . Non bisogna prenderla come una proprietà assoluta: il segno dello pseudoscalare deriva dal numero di dimensioni e dalla segnatura delle basi. Ad esempio in quattro dimensioni lo pseudoscalare al quadrato vale +1, ma se stiamo parlando dello spaziotempo, quindi con una delle basi che quadra a -1, anche in questa algebra lo pseudovettore quadrerà a -1.
. Non bisogna prenderla come una proprietà assoluta: il segno dello pseudoscalare deriva dal numero di dimensioni e dalla segnatura delle basi. Ad esempio in quattro dimensioni lo pseudoscalare al quadrato vale +1, ma se stiamo parlando dello spaziotempo, quindi con una delle basi che quadra a -1, anche in questa algebra lo pseudovettore quadrerà a -1.
Il trivettore
L’elemento nuovo nell’algebra geometrica 3D è definito trivettore ed è interpretabile geometricamente come un elemento di volume orientato. L’orientazione di un volume è data dalla chiralità della terna di trivettori che lo definiscono. Per convenzione diremo che è positiva per una terna destrorsa.
La figura seguente non va presa troppo alla lettera: esattamente come per il bivettore, l’informazione associata è una estensione, un’orientazione ma NON una forma.
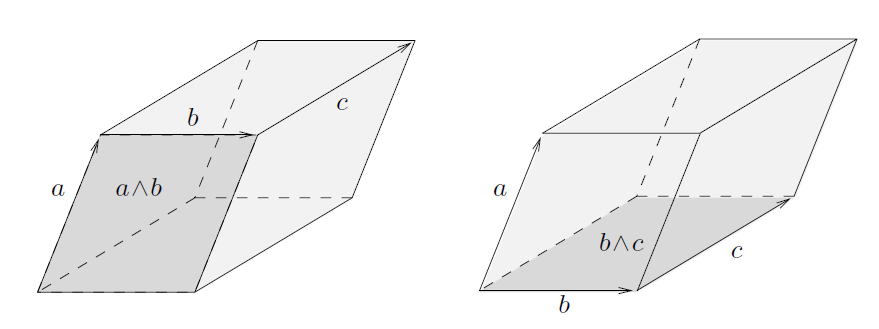
Il trivettore in figura è generato dalla terna destrorsa ![]() ed è sufficiente che un solo vettore cambi verso perché cambi segno l’intero trivettore. Due inversioni, invece, lo lasciano invariato.
ed è sufficiente che un solo vettore cambi verso perché cambi segno l’intero trivettore. Due inversioni, invece, lo lasciano invariato.
Dato che il trivettore è l’elemento di grado più elevato, in questa geometria prende il ruolo di pseudoscalare, che in 2D era riservato al bivettore.
Gli pseudovettori
Cosa succede se moltiplichiamo un vettore per lo pseudoscalare?
Ricordando quello che succede in 2D, saremmo tentati di pensare ad una rotazione di ![]() , ma l’AG è sottile: a prima vista tutto sembra facile, ma quando uno pensa di aver capito, la risposta corretta si rivela molto più ricca di quello che si immaginava.
, ma l’AG è sottile: a prima vista tutto sembra facile, ma quando uno pensa di aver capito, la risposta corretta si rivela molto più ricca di quello che si immaginava.
Meglio allora procedere sotto la guida sicura delle equazioni.
Se si moltiplicano le basi dei bivettori con lo pseudoscalare ![]() otteniamo:
otteniamo:
![]()
![]()
![]()
questa operazione non ruota i vettori, ma li muta nei piani ad essi perpendicolari.
Allora quello che succede in 2D può essere interpretato come una reiezione, vale a dire: moltiplicare un vettore per lo pseudoscalare lo proietta nel sottospazio perpendicolare!
Se questa interpretazione è valida, allora se stavolta moltiplichiamo il bivettore ![]() per lo pseudoscalare
per lo pseudoscalare ![]() dovremmo ottenere il vettore
dovremmo ottenere il vettore ![]() ed effettivamente è così a meno del segno!
ed effettivamente è così a meno del segno!
Questa operazione è detta trasformazione di dualità.
Questo permette di riscrivere i bivettori nell’espressione generale del multivettore come ![]() e quindi:
e quindi:
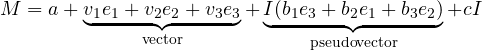
La sottoalgebra pari: i quaternioni
Analogamente a quando visto in 2D, anche in 3D possiamo individuare una sottoalgebra pari, costituita da elementi di grado pari: scalari e bivettori. E’ effettivamente una sottoalgebra perché moltiplicando o sommando questi elementi, otteniamo sempre multivettori di grado pari (chiusura):
![]()
… se a qualcuno fosse venuto il dubbio, gli elementi di grado dispari NON costituiscono una sottoalgebra, infatti ![]()
La sottoalgebra pari in 3D è isomorfa ai quaternioni, entità introdotte da Hamilton nel 1843 come estensioni dei numeri complessi allo spazio tridimensionale.
Vale a pena di soffermarci un po’, anche per illustrare il clamoroso fraintendimento ha impedito una maggiore diffusione dei quaternioni nel mondo scientifico.
Ricapitolando tutti i possibili prodotti degli elementi in 3D:

