Leggere il PDF: Le equazioni di terzo grado – di Salvatore Mattina
Per ricercare geometricamente le soluzioni delle equazioni di terzo grado in forma ridotta ![]() utilizziamo un foglio geogebra che abbiamo predisposto.
utilizziamo un foglio geogebra che abbiamo predisposto.
Analogamente a quanto abbiamo detto per la risoluzione geometrica delle equazioni di secondo grado, avremo due sliders per i coefficienti e altri due per gestire il raggio e l’angolo della nostra incognita.
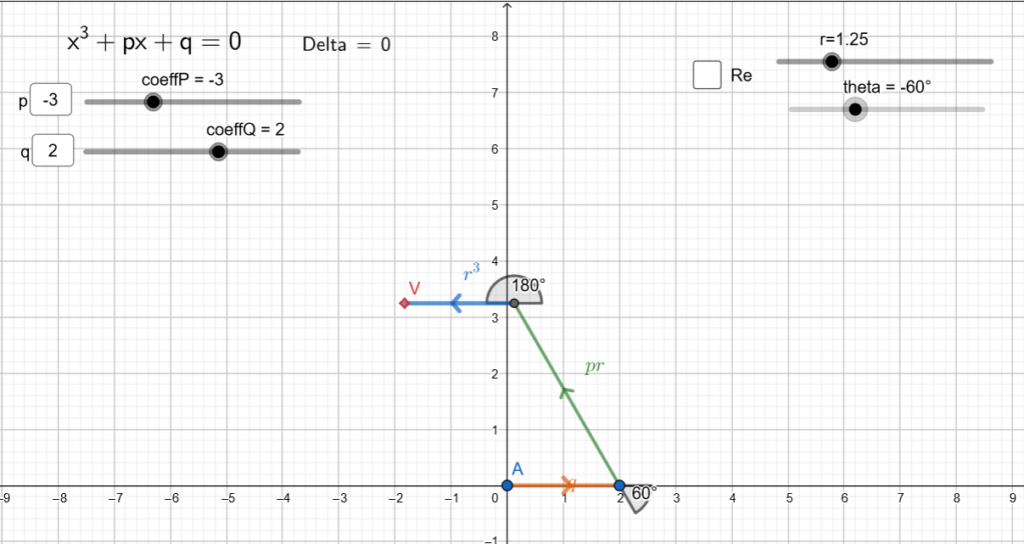
Qualunque sia la combinazione dei coefficienti, notiamo che mentre l’angolo ![]() spazza tutto l’intervallo da
spazza tutto l’intervallo da ![]() a
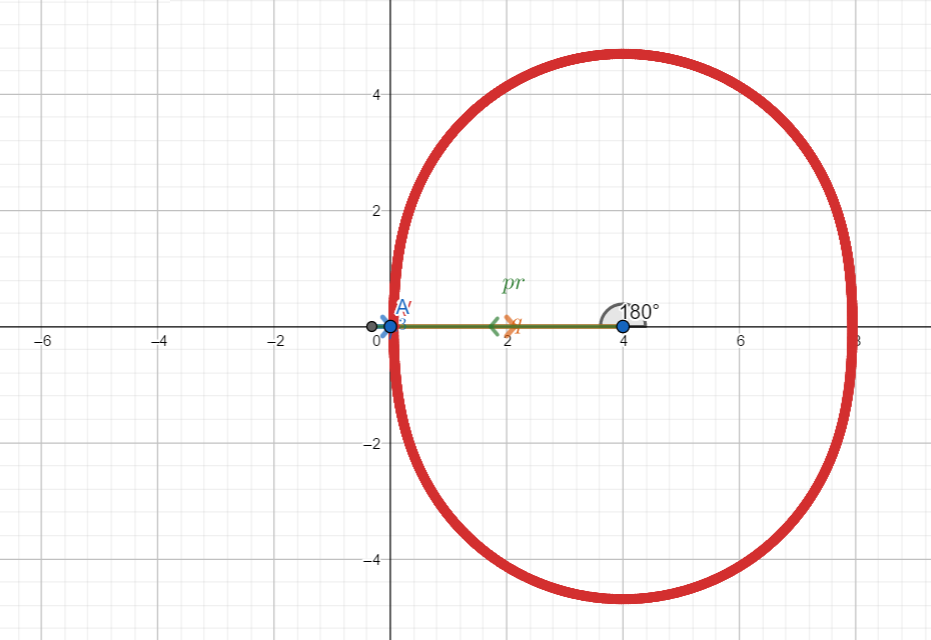
a ![]() , il segmento verde (che corrisponde al termine lineare), compie un giro mentre quello blu (che corrisponde al termine cubico) compie tre giri. La situazione ricorda un poco il sistema tolemaico, con i suoi deferenti e gli epicicli ed infatti la curva descritta dal vertice, con
, il segmento verde (che corrisponde al termine lineare), compie un giro mentre quello blu (che corrisponde al termine cubico) compie tre giri. La situazione ricorda un poco il sistema tolemaico, con i suoi deferenti e gli epicicli ed infatti la curva descritta dal vertice, con ![]() fissato, è una epitrocoide a due lobi.
fissato, è una epitrocoide a due lobi.
Conviene innanzitutto ricercare le soluzioni reali, quindi porre lo slider dell’angolo ![]() sui valori
sui valori ![]() (soluzioni reali positive) e poi
(soluzioni reali positive) e poi ![]() oppure
oppure ![]() per le eventuali soluzioni reali negative. Una volta individuata la soluzione o le soluzioni reali, si potranno ricercare le rimanenti, in accordo con la seguente tabella:
per le eventuali soluzioni reali negative. Una volta individuata la soluzione o le soluzioni reali, si potranno ricercare le rimanenti, in accordo con la seguente tabella:
| soluzioni reali | tre, distinte | tre, almeno due coincidenti | una sola |
Esiste un metodo che semplifica la ricerca delle coppie di soluzioni complesse: basta risolvere questo triangolo:
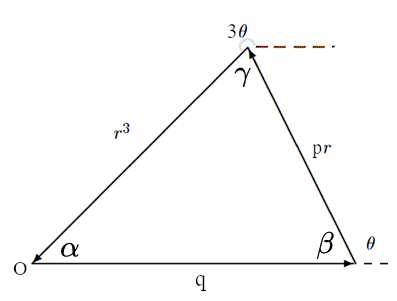
Troveremo che valgono le seguenti relazioni: ![]()
![]()
![]()
quindi la relazione che caratterizza il triangolo soluzione dell’equazione ridotta di terzo grado è ![]()
o anche![]()
e basterà applicare il teorema dei seni per trovare ![]() in funzione di
in funzione di ![]() :
:
![]()
![]()
![]()
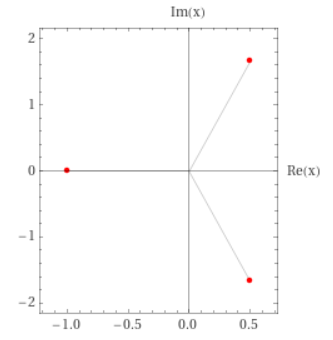
Esempio 1: delta positivo e dunque una sola soluzione reale
![]()
![]()
![]()
![]()
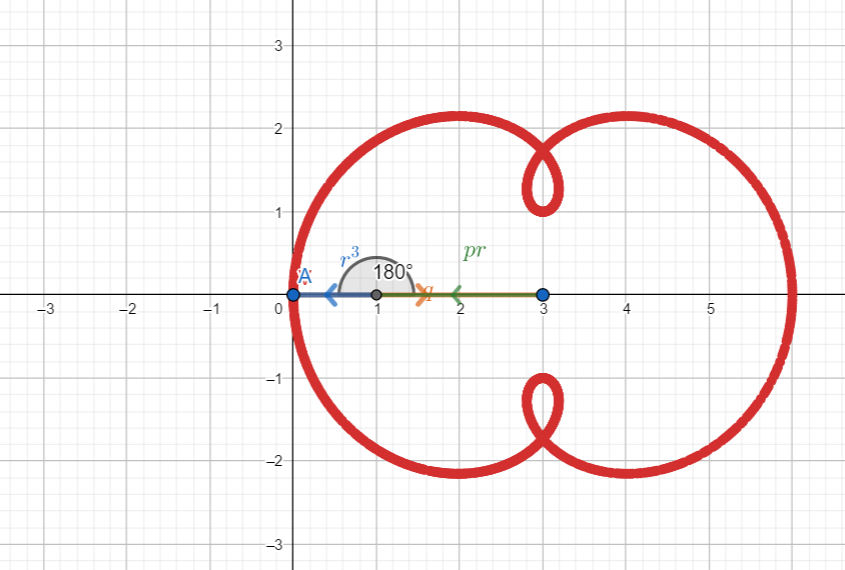
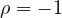
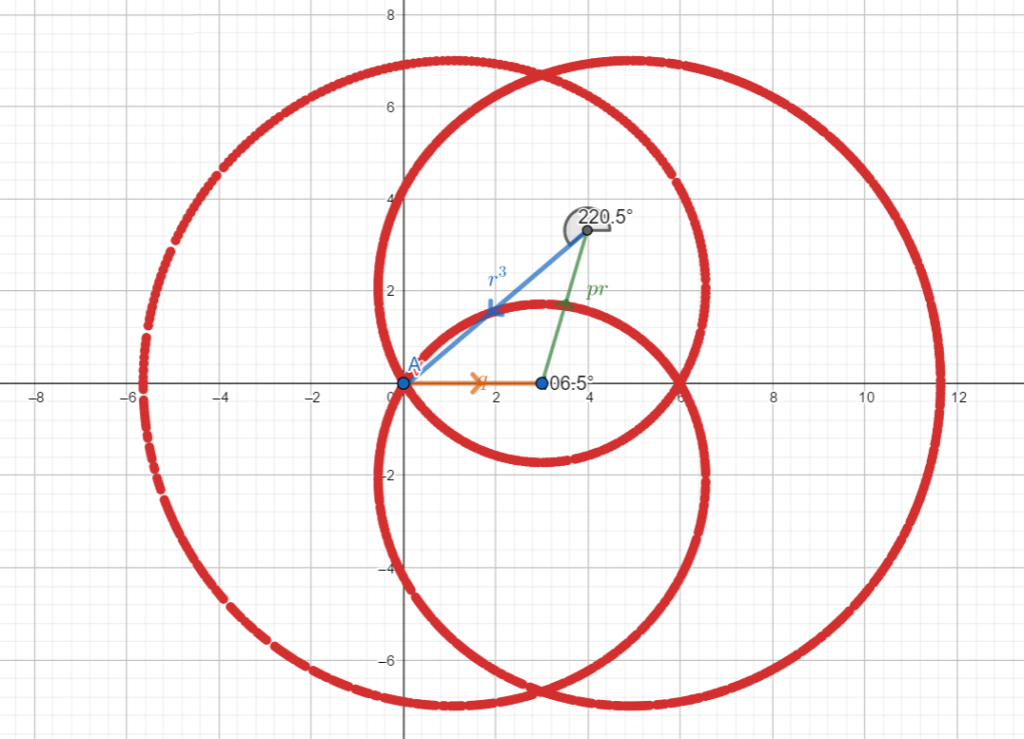
Esempio 2: simile al precedente
![]()
![]()
![]()
![]()
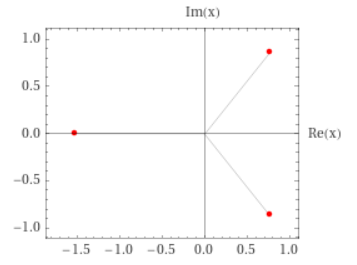
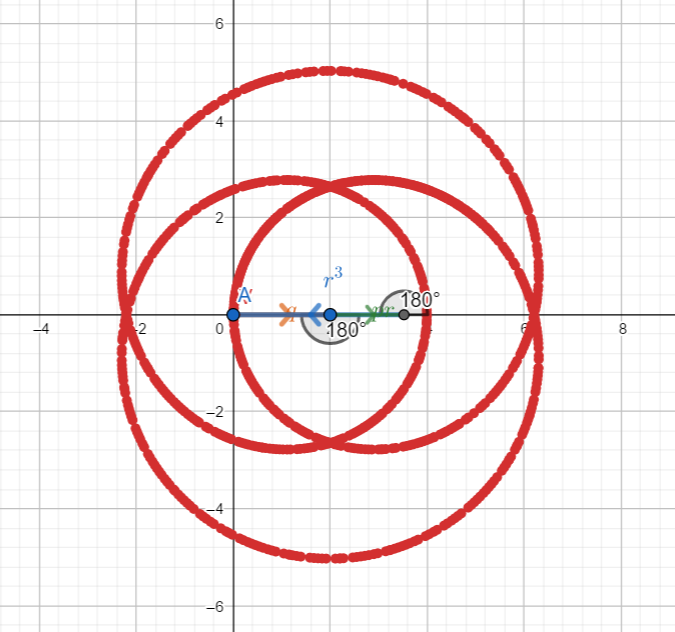
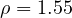
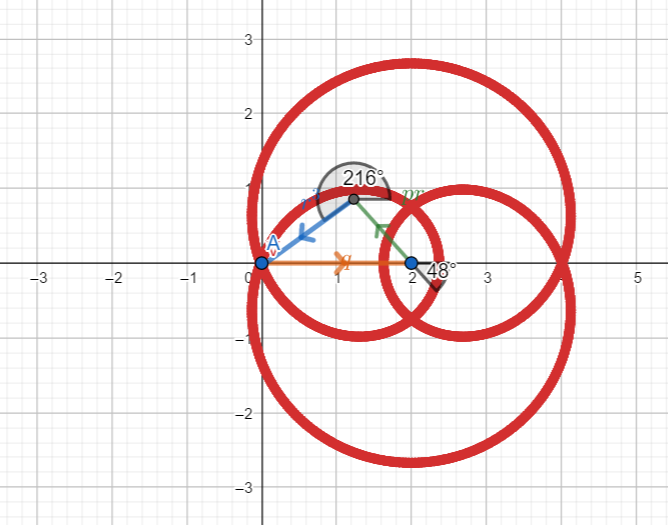
Esempio 3: delta negativo e quindi tre soluzioni reali
![]()
![]()
![]()
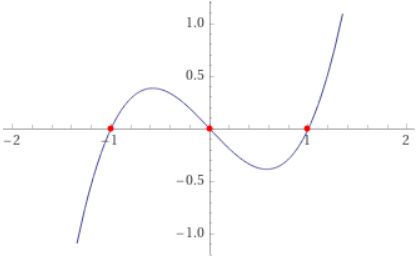
 (derivano da due distinti rami della curva) e la soluzione degenere
(derivano da due distinti rami della curva) e la soluzione degenere 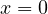
Esempio 4: simile alla precedente ma con tre curve distinte
![]()
![]()
![]()
![]()
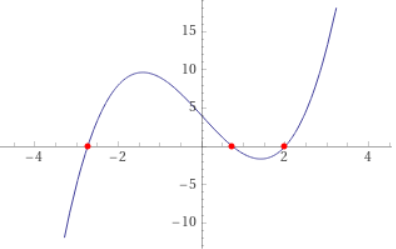
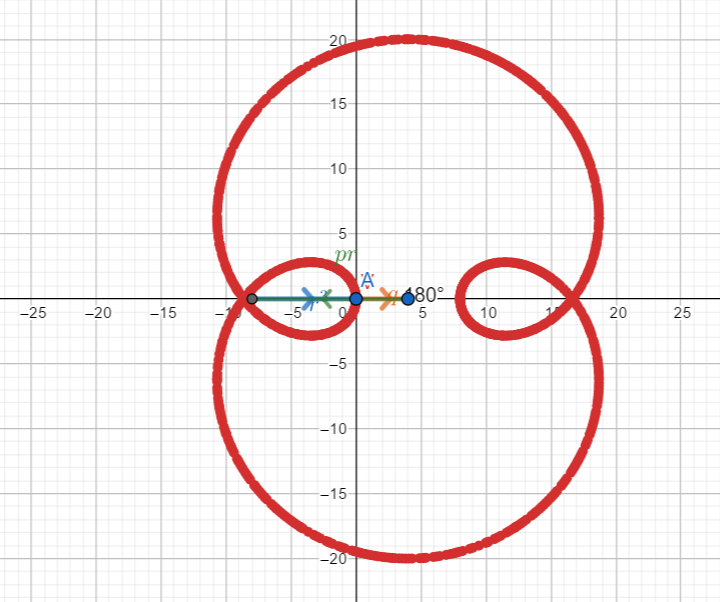
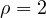
Esempio 5: simile a (1) e (2)
![]()
![]()
![]()
![]()
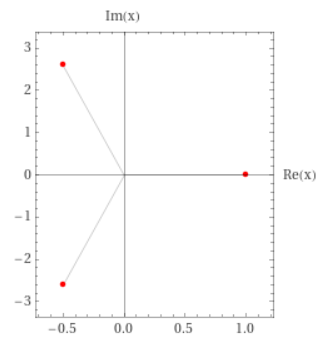
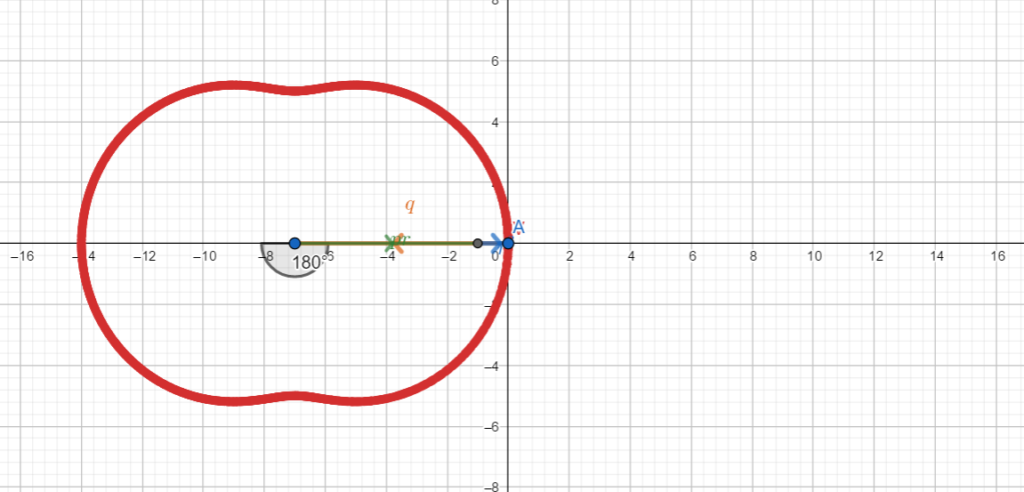
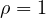
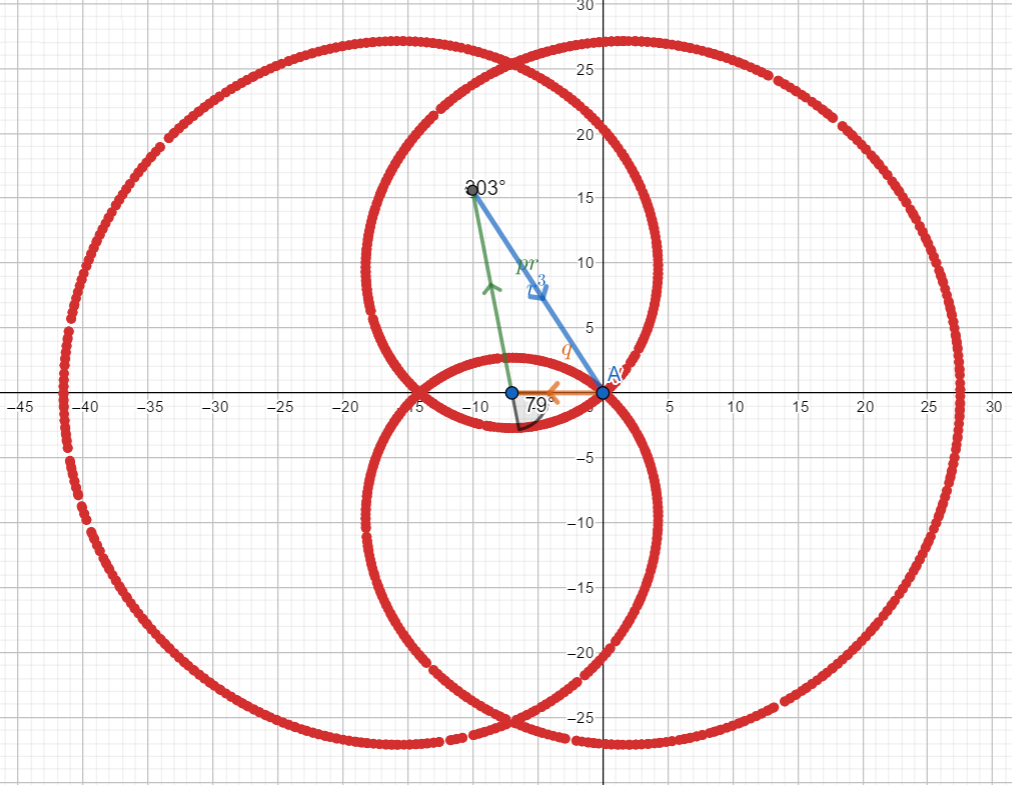
Esempio 6: delta nullo, quindi tre soluzioni reali e almeno due coincidenti
![]()
![]()
![]()
![]()
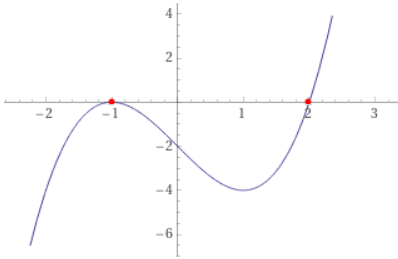
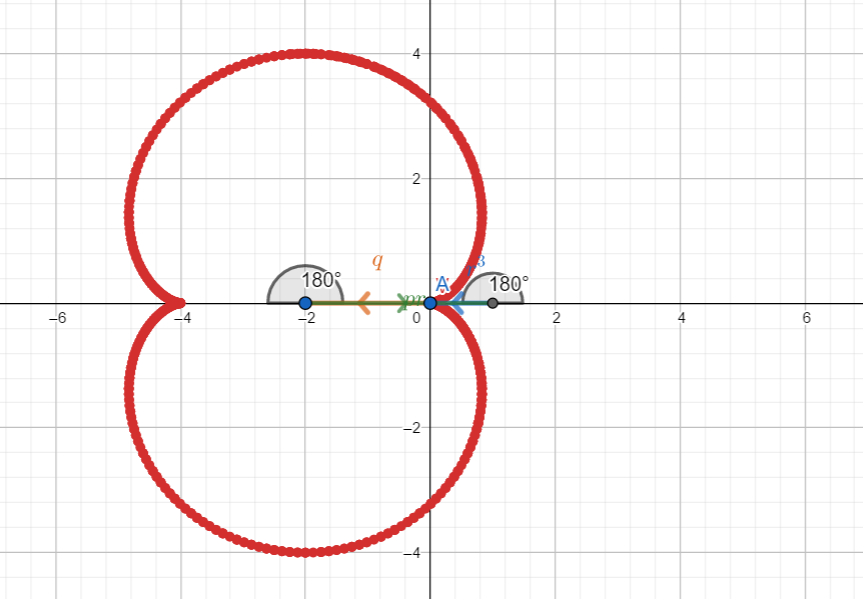
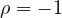 : la curva non mostra un nodo, bensì un punto di stazionamento sull’asse reale, che quindi ha molteplicità doppia. [Dimostrare che in questo caso si tratta di una epicicloide (?)]
: la curva non mostra un nodo, bensì un punto di stazionamento sull’asse reale, che quindi ha molteplicità doppia. [Dimostrare che in questo caso si tratta di una epicicloide (?)]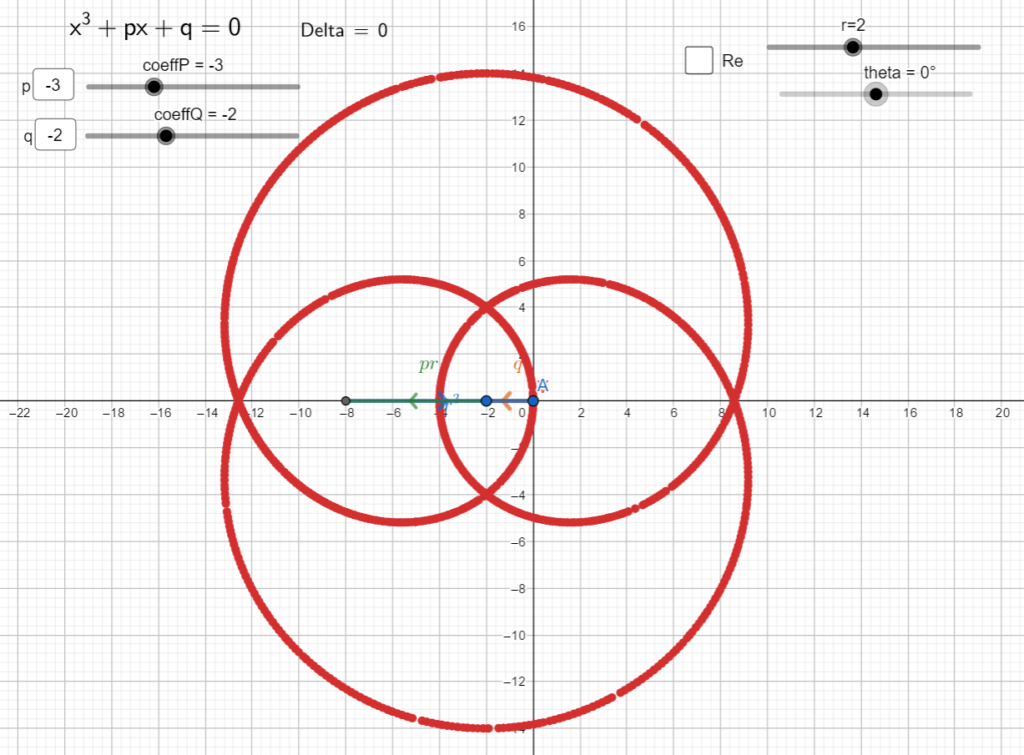
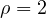
L’unica equazione con tre soluzioni reali coincidenti è nella forma ![]() , che nella trasformazione in forma ridotta diventa
, che nella trasformazione in forma ridotta diventa ![]() la cui soluzione è un punto nell’origine con molteplicità 3.
la cui soluzione è un punto nell’origine con molteplicità 3.
