Un caso particolare e molto interessante di prodotto tra vettori si ha quando i due vettori ![]() e
e ![]() sono unitari, perché li possiamo immaginare appartenenti alla circonferenza unitaria, come in figura:
sono unitari, perché li possiamo immaginare appartenenti alla circonferenza unitaria, come in figura:
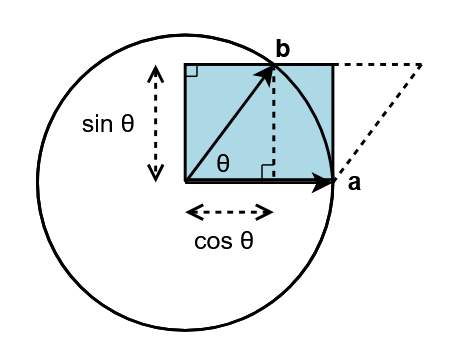
Da questa rappresentazione vediamo che i termini del prodotto geometrico tra i versori ![]() e
e ![]() sono lo scalare
sono lo scalare ![]() ed il bivettore blu, ovvero il parallelogramma dato dall’estensione di
ed il bivettore blu, ovvero il parallelogramma dato dall’estensione di ![]() su
su ![]() che si può ricondurre al rettangolo di altezza
che si può ricondurre al rettangolo di altezza ![]() e quindi:
e quindi:
![]()
Quindi dal prodotto geometrico di due vettori unitari che formano un angolo ![]() nasce un numero complesso di ampiezza unitaria che chiameremo rotore indicato con
nasce un numero complesso di ampiezza unitaria che chiameremo rotore indicato con ![]() perché ha il potere di effettuare una rotazione di angolo
perché ha il potere di effettuare una rotazione di angolo ![]() quando viene moltiplicato (da destra) con altri vettori.
quando viene moltiplicato (da destra) con altri vettori.
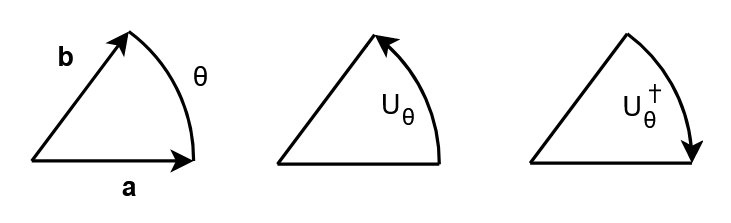
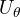 individuato dal prodotto dei due vettori
individuato dal prodotto dei due vettori 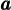 e
e 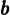 , il suo coniugato
, il suo coniugato 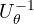 rappresenta la rotazione di senso opposto
rappresenta la rotazione di senso oppostoLa figura identifica il rotore con l’arco orientato, ma potremmo anche identificarlo con il settore circolare, che in effetti si avvicina di più alla nozione di bivettore.
Per la proprietà delle potenze, il prodotto di rotori che giacciono sullo stesso piano equivale ad una rotazione complessiva pari alla somma degli angoli ed è commutativa: ![]()
Dunque il prodotto tra due vettori unitari genera un rotore ![]() , vale a dire un numero complesso che – moltiplicato per un qualsiasi vettore – lo ruota di un angolo
, vale a dire un numero complesso che – moltiplicato per un qualsiasi vettore – lo ruota di un angolo ![]() pari all’angolo compreso tra i due vettori:
pari all’angolo compreso tra i due vettori:![]()
prestando attenzione alla posizione del moltiplicatore, perché determinerà il verso della rotazione.
Ad esempio: ![]()
![]()
ed anche ![]()
(i fattori sono scambiati di posto perché la rotazione avviene nella direzione opposta).
Adesso facciamo una cosa a prima vista molto stupida.
Dividiamo il rotore in due metà, in modo che stiano “a sandwich” col vettore da ruotare e siccome stanno da parti opposte, dovranno avere angoli opposti, e cioè:
![]()
![]()
![]()
![]()
e aggiorniamo la notazione scrivendo in modo più compatto
![]()
dove ![]() è l’inverso (il complesso coniugato) del rotore
è l’inverso (il complesso coniugato) del rotore ![]()
A questo punto, anche per alleggerire un po’, raccontiamo un aneddoto riportato da Luciano De Crescenzo nel suo fortunatissimo “storia della filosofia greca”. L’autore al corso di Analisi e calcolo aveva come docente un vero personaggio: il matematico, poeta e pianista Renato Caccioppoli.
Durante una lezione il professore chiese ad uno studente:
“Sei in cucina, devi cucinarti un piatto di spaghetti. La pentola con l’acqua è sul tavolo di cucina. Il fornello è già acceso. Qual è la prima operazione che fai?”
“Metto la pentola sul fornello” risponde pronto il ragazzo.
“E se la pentola non si trova sul tavolo, ma sul piano della credenza?”
“Fa lo stesso: metto sempre la pentola sul fornello”.
“No: se sei un vero matematico, la metti sul tavolo di cucina e ti riconduci al caso precedente”.
Questo aneddoto fa al caso nostro perché spezzare il rotore in due parti a destra e a sinistra dell’elemento da ruotare sembra un’operazione assurda, proprio come rimettere la pentola sul tavolo, ma ci serve per ricondurci ad un teorema di potenza enorme: ogni rotazione è la composizione di due riflessioni (dovuto ad Hamilton e generalizzato nel teorema di Cartan-Dieudonné).
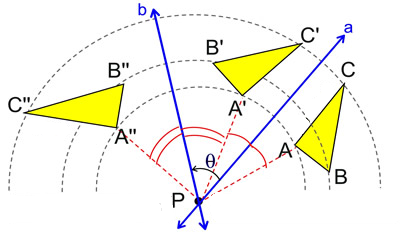
In figura infatti si vede che il triangolo ABC viene riflesso rispetto ad a e successivamente rispetto a b. L’angolo formato da a e b vale metà della rotazione complessiva del triangolo, come si vede considerando gli angoli in P.
Nella seguente app potete giocare con i vettori per verificare questo importantissimo teorema.
Quindi, se vogliamo esprimere una rotazione di angolo ![]() dovremo individuare due vettori nel piano di rotazione che incidono con un angolo
dovremo individuare due vettori nel piano di rotazione che incidono con un angolo ![]() ed esprimere la composizione delle due riflessioni:
ed esprimere la composizione delle due riflessioni:
![]()
o più sinteticamente, visto che il rotore è dato appunto dal prodotto geometrico di ![]() e
e ![]()
![]()
la sequenza simmetrica dei vettori che compongono il rotore viene parafrasata con la simpatica espressione “prima metti i calzini, poi le scarpe, poi togli le scarpe e poi togli i calzini” (socks-shoes property).
Grazie a questo teorema l’espressione ![]() :
:
- è valida in tutte le dimensioni
- funziona in spazi con qualsiasi segnatura (quindi anche nello spaziotempo!)
- ruota qualsiasi elemento di qualsiasi grado
- esprime anche le rotazioni non riferite all’origine
Sarà il caso di imparare a memoria quello che ormai si chiama “prodotto a sandwich”!
Dalla pagina di Marc ten Bosch
Espressione generale del rotore
Un punto d’eleganza dell’algebra geometrica consiste nell’esprimere le trasformazioni senza ricorrere a quegli elementi ausiliari usati così spesso nella geometria classica. Lo abbiamo visto nella critica al prodotto vettoriale, che proietta un vettore perpendicolare al piano dei due fattori.
Ricorrere all’asse per esprimere una rotazione che avviene sul piano ad esso perpendicolare è uno stratagemma che funziona solo in 3D: in dimensioni superiori non funziona più.
Fortunatamente questa limitazione non esiste se ci riferiamo al piano B in cui avviene la rotazione (bivettore) e pertanto esprimeremo il rotore come:
![]()
se la rotazione avviene in senso concorde all’orientazione del piano avremo:
![]()
da confrontare con l’espressione che fa riferimento all’asse di rotazione, che funziona solo in 3D:
![]()
Nella forma “a sandwich” la rotazione nel piano avrà l’espressione:
![]()
