La semplice constatazione che il prodotto vettoriale è rappresentato da un vettore lungo quanto un’area ci fa capire che non abbiamo a che fare con un concetto matematicamente ben fondato.
Il prodotto vettoriale non è invertibile: la sola conoscenza di uno dei due vettori e del prodotto risultante non ci permette di risalire univocamente al secondo vettore.
Infatti, se rappresentiamo due vettori 
e 
ed il loro prodotto vettoriale, ci accorgiamo che possiamo individuare infiniti vettori di lunghezza e direzione diversa che lasciano invariata la quantità 
Questi possibili vettori definiscono una retta (in verde).
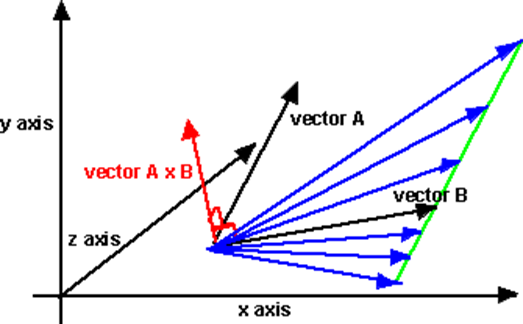
E ancora: il prodotto vettoriale funziona solo in 3D (richiedendo la terza dimensione per il vettore risultante). In dimensioni superiori non è neppure definito perché ci sono infiniti vettori perpendicolari ad un piano dato.
Altro svantaggio: il prodotto vettoriale non è associativo e non è dotato di elemento neutro, infatti non esiste alcun vettore 
tale che 
Vi sono poi alcune riflessioni:
Perché mai introdurre un vettore perpendicolare al piano individuato dai due fattori?
Perché è necessaria la regola della mano destra? La Natura in qualche modo predilige le terne destrorse rispetto a quelle sinistrorse? Eppure sappiamo che la fisica è totalmente simmetrica, a parte un caso particolarissimo!
Il calcolo del prodotto vettoriale in base alle componenti si ottiene agevolmente impostando la seguente matrice e calcolando il determinante:
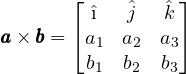
per semplificare, diciamo che i due vettori giacciono nel piano 
e quindi l’unica componente non-nulla sarà la 
, proprio come ci aspettiamo ed i coefficienti saranno in forma mista con alternanze di segni:
Se invece i due vettori da moltiplicare non giacciono nel piano, allora l’espressione completa sarà:
