Opposto, coniugato, inverso – Algebra geometrica

Per completare adeguatamente la descrizione dell’algebra geometrica, accanto all’Aufbau col quale vengono costruiti gli elementi, bisogna anche descrivere the dark side: ovvero gli elementi in qualche modo negativi di un generico multivettore $M = a + \pmb{v} + B + bI$ .
Questo è essenziale per la correttezza di alcune operazioni, ad esempio la divisione o la rotazione in senso opposto.

Questa pagina può essere noiosa o interessante. Se guardata dal lato algebrico, è indubbiamente noiosa. Invece, se guardata dal lato geometrico, è molto interessante. La cosa divertente è che si tratta degli stessi concetti, che nell’AG sono interpretabili in senso algebrico o spaziale, ma la loro radice è comune.

Opposto

Il costrutto negativo più elementare di un multivettore è l’opposto, che vede mutare di segno tutti i suoi elementi: $-M = - a - \pmb{v} - B - bI$

Coniugato (reverse)

Definiamo coniugato il multivettore $M^ \dagger$ ( $\dagger$ è il simbolo chiamato dagger o anche obelisco) altre volte indicato con $M^{\sim}$ nel quale tutti i termini che si sommano nel generico multivettore vedono invertito l’ordine dei loro fattori. Ecco alcuni esempi:

Dal punto di vista del calcolo, occorre ricordare che il coniugio è una operazione ricorsiva: $(ab)^\dagger = b^\dagger a^\dagger$

L’operazione di coniugio lascia ovviamente invariati scalari e vettori, mentre cambia il segno di bivettori e trivettori. Come si intuisce, il pattern per i diversi gradi è il seguente: + + – – + + – – …

Il multivettore generico
$M = a + \pmb{v} + B + bI$
viene trasformato per coniugazione nel multivettore
$M^\dagger = a + \pmb{v} - B - bI$

Inverso

Per quanto abbiamo appena detto,

$A^\dagger A = AA^\dagger = a_n ... a_3 (a_2 (a_1a_1) a_2) a_3 ... a_n =$
$|a_1|^2 (a_n … (a_3 (a_2a_2) a_3) … a_n =$
$= |a_1|^2 + |a_2|^2 + |a_3|^2 + ... + |a_n|^2$

che è un numero reale, utilissimo se vogliamo calcolare l’inverso di un multivettore M, infatti:

$M^{-1} M = 1$
$M^{-1} M M^\dagger = M^\dagger$
e quindi

$\begin{equation} M^{-1}=\frac{M^\dagger}{MM^\dagger} = \frac{M^\dagger}{|M^2|}$

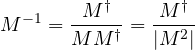
Da notare che l’inverso di un vettore base coincide con la base stessa: $e_x^{-1} = e_x^\dagger / |e_x|^2 = e_x$

Abbiamo detto che l’AG è superiore a quella che viene insegnata comunemente perché ha una definizione ben fatta di prodotto tra vettori, che è anche invertibile. L’inverso di un vettore è ciò che moltiplicato per il vettore stesso riporta all’unità:

$\begin{equation} \pmb{v}\pmb{v}^{-1}=1=\pmb{v} \frac{\pmb{v}}{|\pmb{v}|^2}$

Agli studenti più svegli non sarà sfuggita questa stranezza: quando si parla dell’inverso di un numero complesso, invece, l’espressione è data da:

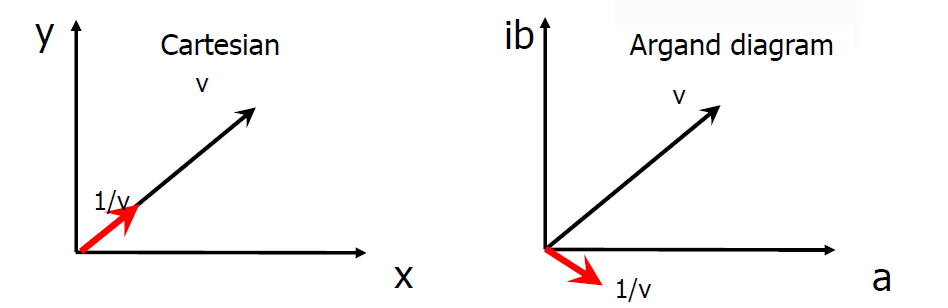
$\begin{equation} \frac{1}{z} = \frac{1}{(a+ib)} = \frac{1}{a^2+b^2}(a-ib)$

e vediamo bene che il fattore di riduzione è lo stesso, ma in questo caso al numeratore abbiamo il coniugato!
Graficamente la differenza è lampante: motivo in più per convincersi che i numeri complessi sono qualcosa di radicalmente diverso da un vettore e quindi non vanno confusi per nessun motivo.

L’inverso di un vettore e di un numero complesso mostrano che NON si tratta dello stesso oggetto geometrico

Esercizio: calcoliamo l’inverso di un vettore. Prendiamo due vettori:

$\pmb{a} = e_1 + 2 e_2$
$\pmb{b} = 3 e_1 + 2 e_2$

Il loro prodotto scalare vale $\pmb{a} \cdot \pmb{b} = a_1b_1 + a_1b_2 = 3 + 4 = 7$
Il loro prodotto wedge vale $\pmb{a} \wedge \pmb{b} = -4 e_1e_2$
Il loro prodotto geometrico dunque vale $\pmb{a} \pmb{b} = 7 - 4 e_1e_2$
Dal prodotto possiamo ricavare $\pmb{b}$ conoscendo $\pmb{a}$ come segue:

$\begin{equation} b = a^{-1}(ab) = \frac{e_1 + 2 e_2}{5} (7 - 4 e_1e_2) = 3 e_1 + 2 e_2$

$M_1 = e_2e_3e_4$	$M_1^ \dagger = e_4e_3e_2$
$M_2 = P+(Q \wedge R)$	$M_2^ \dagger = P + (R \wedge Q)$
$B = \pmb{a} \wedge \pmb{b}$	$B^\dagger = -B$