La potenza elettrica in regime alternato

I numeri complessi, da strumenti malsopportati e accompagnati da un assurdo misticismo, divennero uno strumento incredibilmente utile con l’avvento dell’energia elettrica alternata. Questo avvenne verso la fine dell’800 soprattutto per opera di Charles “Proteus” Steinmetz, scienziato poco conosciuto al pubblico, ma che per genialità era alla pari dei ben più celebri Edison e Tesla.

Infatti le grandezze sinusoidali tensione e corrente:

$v(t) = |V| \sin(\omega t +\phi_V)$
$i(t) = |I| \sin(\omega t +\phi_I)$

possono essere rappresentate da un fasore, ovvero un numero complesso che viene immaginato in continua rotazione con velocità $\omega = 2 \pi f$ , generando sull’asse reale una sinusoide.

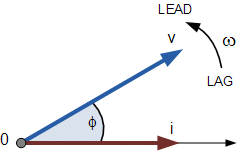
Il fasore prende questo nome perché, congelando la situazione in un dato istante, si vedono immediatamente le relazioni di fase tra le grandezze elettriche. Ad esempio nella figura seguente si vede che la corrente è in ritardo rispetto alla tensione (i vettori sono immaginati in rotazione antioraria). L’angolo di sfasamento è $\phi$ e negli impianti di trasmissione dell’energia elettrica va ridotto il più possibile perché altrimenti la potenza sfruttabile dalla linea si riduce.

La potenza elettrica è un numero complesso $S$ che si ottiene moltiplicando tensione e corrente, il problema è che spesso si legge la formula $S = VI$ la quale funziona perfettamente per il grafico qui sopra. Peccato che NON sia la formula corretta e questa illusione deriva dal fatto che la corrente $I$ si trova sull’asse reale e quindi coincide col suo coniugato!

La formula corretta dovuta a Steinmetz, infatti, è $S = VI^*$ ma per decenni la sua spiegazione è stata totalmente incompresa (approccio ingegneristico alla “funziona, ma non sappiamo perché”).

La radice dell’errore sta nel fatto che continuamo a trattare i numeri complessi come vettori, ma l’algebra geometrica insegna che le basi sono diverse nei due approcci: nell’approccio complesso stiamo parlando di un multivettore composto da uno scalare ed un bivettore $e_1_2$ , mentre nell’approccio vettoriale siamo in uno spazio vettoriale ordinario formato dalle basi $e_1$ ed $e_2$ .

Proviamo, allora, a confrontare diversi approcci al problema, quando V ed I sono dati nelle forme:

Potenza secondo Steinmetz (pubblicazioni tra il 1893 ed il 1899):
$P = (ac+bd) + j (bc-ad)$
funziona, ma i tentativi di spiegazione del grande elettrotecnico sono traballanti: V ed I sono trattati come numeri complessi ma per le potenze, dato che hanno frequenza doppia, varrebbe $j^2=+1$ con $j$ non commutativo ( $ja \neq aj$ , così come $VI \neq IV$ )

Prodotto tra numeri complessi:
$VI = (ac - bd) + i (bc + ad)$
numericamente errato in generale, funziona – come abbiamo detto sopra – solo nel caso $d=0$ (corrente sull’asse reale)

Prodotto geometrico:
$VI = V \cdot I + V \wedge I = (ac+bd) + (ad-bc) e_1_2$
coincide a meno del segno della parte immaginaria

Prodotto tra numeri complessi, ma col coniugato del secondo fattore:
$VI^* = (ac + bd) + i (bc - ad)$
coincide!

Prodotto tra numeri complessi, ma col coniugato del primo fattore:
$V^* I = (ac + bd) + i (ad - bc)$
coincide col prodotto geometrico, ma non con la formula di Steinmetz (a meno del segno meno della parte immaginaria).

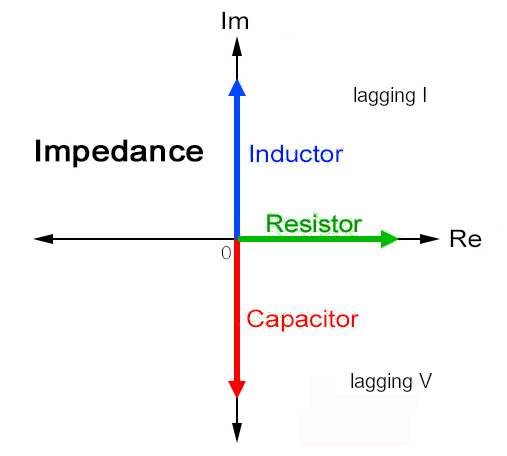
Per amor di completezza, va detto che Guilbert nel 1893 propose una modifica alla formula di Steinmetz, ovvero di invertire l’asse immaginario, per armonizzare la notazione con quella correntemente in uso, che vede la reattanza induttiva sul semiasse immaginario positivo e quella capacitiva sull’asse negativo, ovvero la convenzione che vede la reattanza positiva quando la corrente è in ritardo rispetto alla tensione.
Così facendo, avremmo la coincidenza della formula della potenza elettrica col prodotto geometrico!

Convenzione dei segni per la resistenza complessa (impedenza)

Perché occorre moltiplicare per il coniugato di uno dei fattori? Per rendere il risultato dipendente solo dall’angolo di fase tra i due! Altrimenti, dipenderebbe dalla fase assoluta.
Vediamone la spiegazione, che illustra egregiamente anche il motivo della coincidenza del risultato con il prodotto geometrico.

Siano dati due numeri complessi identificati dai due vettori a e b, che formano un angolo $\theta$ .
Il triangolo grigio ha come lati la proiezione di b su a e sulla sua perpendicolare.

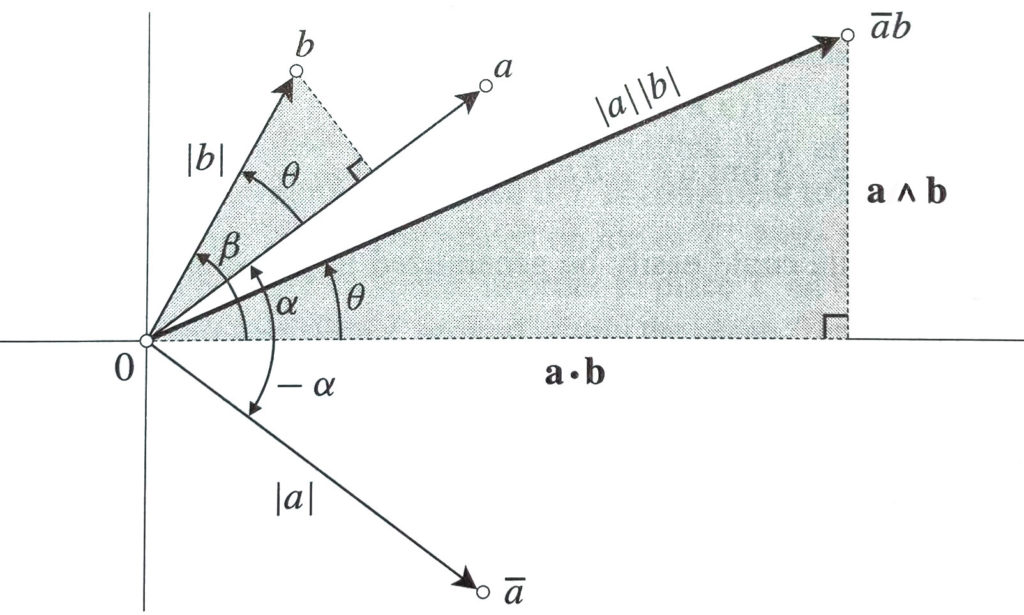
Figura tratta da “Visual complex analysis”, p. 29

Se ora moltiplichiamo b per il coniugato di a, ricordando l’interpretazione amplitwist del numero complesso, otterremo un altro triangolo ruotato di $-\alpha$ e scalato di un fattore $|a|$ .
Pertanto il cateto maggiore andrà sull’asse orizzontale e la sua misura varrà $|b|\: \cos \theta\:|a|$ ovvero il prodotto scalare $a \cdot b$ . Il cateto minore si troverà parallelo all’asse y e la sua misura varrà $|b|\: \sin \theta\: |a|$ ovvero l’area del prodotto esterno $a \wedge b$ .
Otteniamo così la relazione $a^*b = a \cdot b + a \wedge b$

In conclusione, con questo esempio vediamo molto bene che l’approccio dell’algebra geometrica riesce ad includere elegantemente gli aspetti geometrici che si sarebbero dovuti aggiustare ad hoc (coniugazione di uno dei fattori).

Come vettori	Come numeri complessi	Come elementi dell’AG
$\pmb{V} = a e_1 + b e_2$	$V = a + ib$	$V = a+ b e_1e_2$
$\pmb{I} = c e_1 + d e_2$	$I = c + id$	$I = c + d e_1e_2$
$\pmb{V} \pmb{I} = (ac+bd) + (ad-bc) e_1_2$	$VI = (ac - bd) + i (ad + bc)$	$VI = (ac - bd) + (ad + bc) e_1_2$
		(numeri complessi generalizzati)