Electrical power in alternating current

Complex numbers, from ill-tolerated tools accompanied by absurd mysticism, became an incredibly useful tool with the advent of alternating electricity. This happened towards the end of the 19th century mainly thanks to Charles “Proteus” Steinmetz, a scientist little known to the public, but who was as genius as much more famous Edison or Tesla.

In fact, the voltage and current sinusoidal quantities:

$v(t) = | V | \sin (\omega t + \phi_V)$
$i(t) = | I | \sin (\omega t + \phi_I)$

can be represented by a phasor , that is a complex number that is imagined in continuous rotation with speed $\omega = 2 \pi f$ , generating a sinusoid on the real axis.

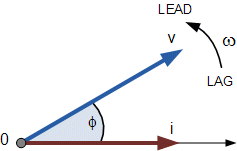
The phasor takes this name because, by freezing the situation at a given instant, the phase relationships between the electrical quantities are immediately seen. For example, in the following figure we see that the current is lagging behind the voltage (the vectors are imagined in counterclockwise rotation). The phase shift angle is $\phi$ and in electrical power transmission plants it must be reduced as much as possible because otherwise the usable power from the line is reduced.

Electric power is a complex number $S$ that is obtained by multiplying voltage and current, the problem is that we often read the formula $S = VI$ which works perfectly for the graph above. Too bad it is NOT the correct formula and this illusion derives from the fact that the current $I$ is on the real axis and therefore coincides with its conjugate!

The correct formula, due to Steinmetz, in fact, is $S = VI^*$ but for decades his explanation has been totally misunderstood (the classical engineering attitude “it works, but we don’t know why”).

The root of the error lies in the fact that we continue to treat complex numbers as vectors, but geometric algebra teaches that the bases are different in the two approaches: in the complex approach we are talking about a multivector composed of a scalar and a bivector $e_1_2$ , while in the vectorial approach we are in an ordinary vector space formed by the bases $e_1$ and $e_2$ .

Let’s try, then, to compare different approaches to the problem, when V and I are given in the forms:

Power according to Steinmetz (publications between 1893 and 1899):
$P = (ac+bd) + j (bc-ad)$
it works, but the great electrical engineer’s attempts at explanation are shaky: V and I are treated as complex numbers but for powers, since they have double frequency, it would be $j^2 = + 1$ with non-commutative $j$ ( $ja \neq aj$ , as well as $VI \neq IV$ )

Product between complex numbers:
$VI = (ac - bd) + i (bc + ad)$
numerically incorrect in general, it works – as we said above – only in the case $d = 0$ (current on the real axis)

Geometric product:
$VI = V \cdot I + V \wedge I = (ac + bd) + (ad-bc) e_1_2$
coincides up to the sign of the imaginary part

Product of complex numbers, but with the conjugate of the second factor:
$VI^* = (ac + bd) + i (bc - ad)$
coincides!

Product of complex numbers, but with the conjugate of the first factor:
$V^* I = (ac + bd) + i (ad - bc)$
coincides with the product geometric, but not with Steinmetz’s formula (unless the minus sign of the imaginary part).

For the sake of completeness, it must be said that in 1893 Guilbert proposed a modification to Steinmetz’s formula, that is to invert the imaginary axis, to harmonize the notation with the one currently in use, which sees the inductive reactance on the positive imaginary semi-axis and the capacitive one on the ‘negative axis, that is the convention that sees the positive reactance when the current lags behind the voltage.
Doing so, we would have the coincidence of the formula of electric power with the geometric product!

Convention of signs for complex resistance (impedance)

Why do we need to multiply by the conjugate of one of the factors? To make the result dependent only on the phase angle between the two! Otherwise, it would depend on the absolute phase.
Let’s see the explanation, which also illustrates the reason for the coincidence of the result with the geometric product.

Given two complex numbers identified by the two vectors a and b , which form an angle $\theta$ .
The gray triangle has the projection as sides of b on a and its perpendicular.

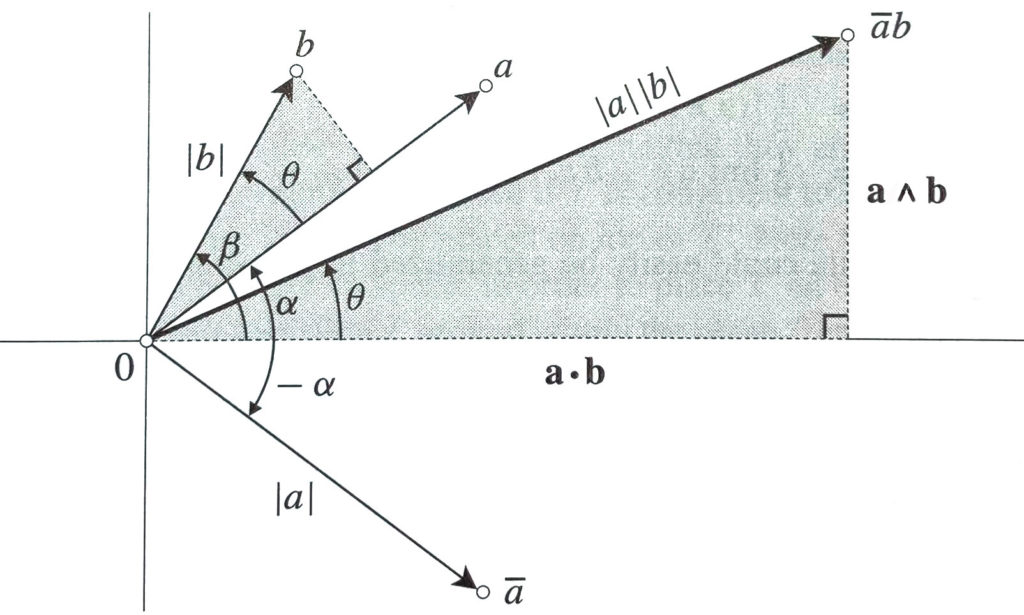
Figure excerpt from “Visual complex analysis”, p. 29

If we now multiply b by the conjugate of a, remembering the amplitwist interpretation of the complex number, we will get another triangle rotated by $- \alpha$ is scaled by a factor $|a|$ .
Therefore the major cathetus will go on the horizontal axis and its measure will be $| b | \: \cos \theta \: | a |$ or the dot product $a \cdot b$ . The minor cathetus will be parallel to the y axis and its measure will be $| b | \: \sin \theta \: | a |$ or the area of the external product $a \wedge b$ .
We thus obtain the relation $a^* b = a \cdot b + a \wedge b$

In conclusion, with this example we see very well that the geometric algebra approach manages to elegantly include the geometric aspects that should have been adjusted ad hoc (conjugation of one of the factors).

As vectors	As complex numbers	As GA elements
$\pmb{V} = a e_1 + b e_2$	$V = a + ib$	$V = a+ b e_1e_2$
$\pmb{I} = c e_1 + d e_2$	$I = c + id$	$I = c + d e_1e_2$
$\pmb{V} \pmb{I} = (ac+bd) + (ad-bc) e_1_2$	$VI = (ac - bd) + i (ad + bc)$	$VI = (ac - bd) + (ad + bc) e_1_2$
		(generalized complex numbers)