The elements of degree one, called vectors, are added with the classic rule of the parallelogram, that is, the components are added algebraically.
For the elements of degree two, called bivectors, it is necessary to proceed with more caution.
A bivector is an oriented portion of the plane, therefore it is characterized by a magnitude (the measure of the area), a direction (given from the circulation) and the orientation in space. It sounds surprising, but the bivector has no shape !
In fact it can be thought of as a rectangle or a circle or any other shape useful for summing purpose.
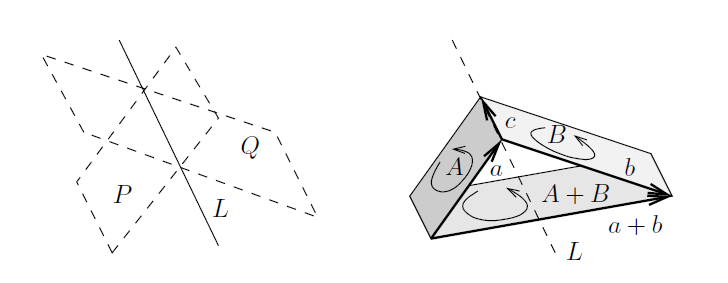
Imagine that we need to add two bivectors A and B, which lie on two planes P and Q that meet along the line L.
We can reshape A and B so that they are generated by a common vector 
, then:
It will then result
Next to the concept of sum we can see, thanks to Marc ten Bosch page, the projection of a bivector to get its components. The outer product of the two vectors 
and 
generates a bivector in three-dimensional space (in blue). This can be projected into the fundamental planes by obtaining the three component bivectors (in orange, purple and yellow).
Try moving points a and b and see how the projections change. The components of the vectors can be fixed by writing them directly in the white boxes. It is also possible to rotate the viewpoint to better understand the geometric relationships between the elements.
Recalling the external products of the versors:
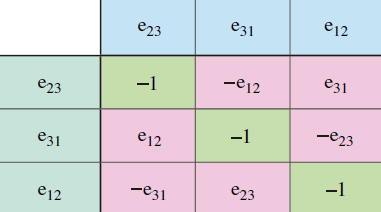
we will finally obtain that the blue bivector 
has as components:
Exercise: verify that 