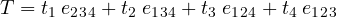Some physics texts, alongside classical vectors (also called polar ) introduce axial vectors, also called pseudovectors. They are defined as those vectors that manifest their physical effects in a plane perpendicular to them.
Typical examples are angular velocity and torque.
The singular aspect is that there is no difference in notation: they are indicated in the same way despite having a radically different meaning.
J.D. Jackson in his “Classical electrodynamics” points out “ We see here… A dangerous aspect of our usual notation. The writing of a vector as ‘a‘ does not tell us whether it is a polar or an axial vector ”.
… for the sake of completeness, we report that french textbooks usually indicate axial vectors by superimposing a curved arrow on the letter:
How do we distinguish between a normal and an axial vector? The same way we distinguish vampires from normal people: with a mirror.
If a ball is moving in a direction perpendicular to the mirror, looking at its reflected image we will see it moving in the opposite direction, so we can say that the mirror reverses the velocity vector.
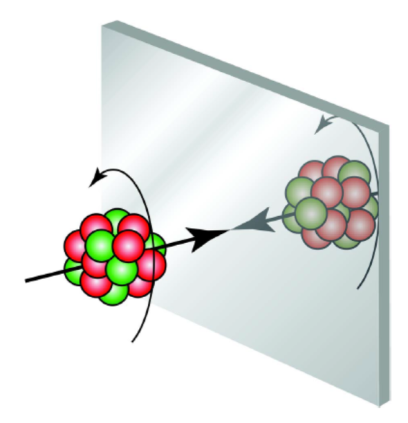
If the ball is rotating counterclockwise in front of the mirror, its image will also rotate in the same direction. The axial vector ![]() (angular velocity), like vampires, is NOT reflected in the mirror.
(angular velocity), like vampires, is NOT reflected in the mirror.
Getting serious again, this is a glaring case of how classical physics needs to change some of its basic definitions. It is quite clear that the axial vectors are actually bivectors.
- axial vectors arise from a vector product or from a rotor of a vector field
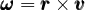
bivectors arise from an external product which, as we have seen, is the dual of the vector product
- axial vectors remain unchanged under spatial inversion (
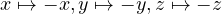 ):
): 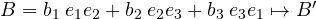
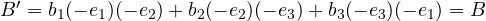
- axial vectors are closed with respect to the sum (like bivectors) but the sum of a polar vector with an axial one results in an entity that can still be defined as a vector according to physics, but does not respect the rules on spatial inversion. The violation of CP symmetry at the nuclear level can be traced back to the sum of an axial vector (the spin) with a vector
- in a space of dimension
 the elements of order
the elements of order  (which have
(which have  bases, each of which is formed by the outer product of all but one bases) behave as pseudovectors.
bases, each of which is formed by the outer product of all but one bases) behave as pseudovectors.
For example, in 4 dimensions the pseudovectors are the trivectors