Hamilton wanted to extend the complex numbers expressed as 
and represented in the Argand-Gauss plane into three-dimensional space, but he didn’t succeed. He then proposed a four-dimensional object of the form 
where 
, 
and 
are symbols that behave like the imaginary unit 
.
The fundamental property of quaternions came to Hamilton in a flash of genius during a walk and was so important that it was carved on a stone plaque placed on Broom bridge near Dublin: 
The importance of quaternions is linked to the fact that they are able to represent rotations in three-dimensional space, turning an apparent problem (their non-commutativity) into a spectacular demonstration of correctness, because also 3D rotations are not commutative.
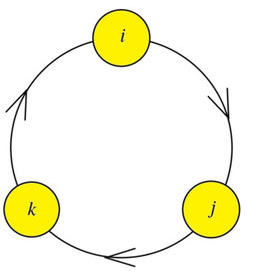
We observe that the relationships between the bases of the quaternions and the bases of the bivectors are perfectly superimposable, as long as we relate them as follows:
| most common convention (one sign change only) | alternative convention (three changes of sign) |
   |   |
the minus sign derives from the fact that Hamilton conceived the bases as a left-handed system, while the system currently in use is right-handed (positive angles counterclockwise). For this reason one of the bases must change sign (or three).
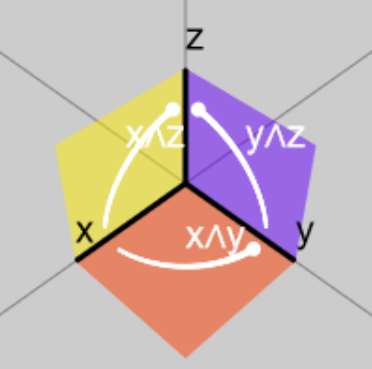
The success of the quaternions led Hamilton to venture to identify the three bases i , j and k with the three bases of vector space 3D: he called them pure quaternions , that is, those without a scalar part. Indeed, it was he who coined the expression vector and still today the symbols i , j and k are used to indicate the versors of 3D space.
However – as we said at the beginning – Maxwell noted that the kinetic energy expressed by means of the quaternions intended as vectors was negative: which was unacceptable.
A few years later, Minkowski also found himself having to express Einstein’s spacetime in four dimensions, but instead of using quaternions, he preferred the vector formalism of Gibbs and Heaviside. The quaternions, therefore, soon fell into oblivion and were rediscovered only with the advent of computer graphics and the need to model 3D rotations on the computer.
Today we can finally understand the incredible misunderstanding that arose: the three bases of the quaternions are to be understood as bivectors and therefore it is clear that they are able to model rotations, but they should not be considered as vector space ! In a way … they were all right.
These two worlds are brought together in the eight dimensions of 3D geometric algebra.
We could continue with the study of quaternions, but we do not do it because geometric algebra – once again – manages to include and illuminate this topic as well, making it understandable.
We will then talk about 3D rotors, of which we can say that quaternions are the … blurred form (see the page Let’s remove quaternions from every 3D engine by Marc Ten Bosch).