The scalar product between two vectors is given by the modulus of the first by the component of the second along the first (projection), but since it is a symmetrical bilinear form, the inverse is also valid, i.e. the projection of the first on the second.
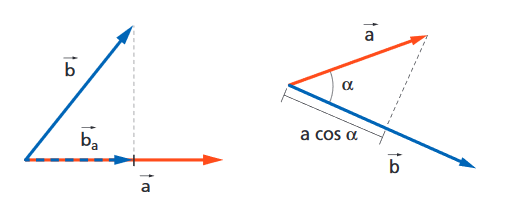
The dot product combines two vectors into a scalar quantity, which immediately suggests that the richness of their spatial information is lost.
In fact, if we represent two vectors 
and 
, and the projection of over , we realize that we can identify infinite vectors of different length and direction, which leave the projection unchanged.
Extending the reasoning in three dimensions, we realize that the locus of vectors with a given projection on is a plane perpendicular to and passing through the extreme of the projection on .
From the algebric point of view, the calculation of the scalar product is simple: it is the sum of the products of the index-paired components:
In short, the scalar product captures only one side of the relationship between two vectors: how much they are aligned. Everything else is left out — the plane that contains them, its orientation, the area they span. No surprise, then, that physics had to introduce a second product to recover that information: the cross product (whose own limitations we will examine in turn). Geometric algebra will do better, reuniting the two halves into a single, invertible operation: the geometric product.