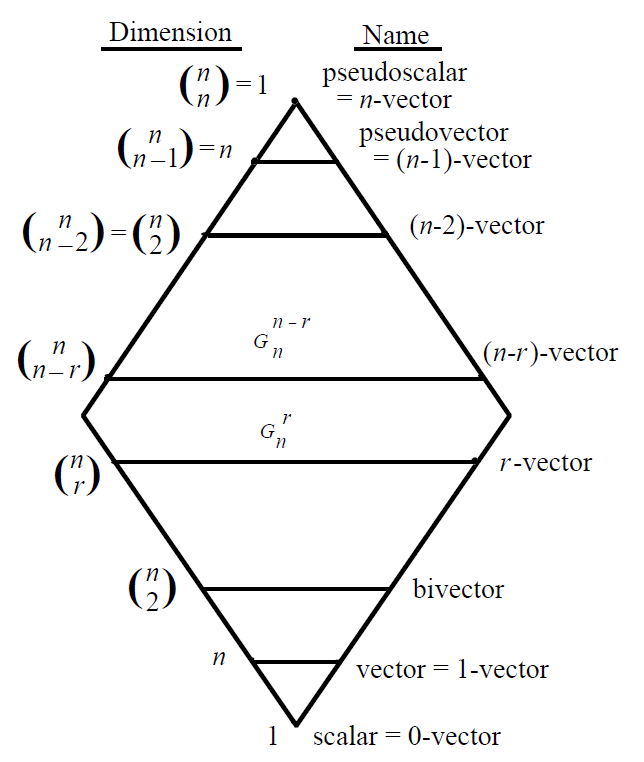
The number of bases of the various grades of a geometric algebra of dimension ![]() is obtained from row
is obtained from row ![]() of Pascal’s triangle. This structure is symmetrical and therefore, just as there is only one type of scalar, we will have only one basis for the element of maximum degree which will take the name of pseudoscalar, regardless of the dimension
of Pascal’s triangle. This structure is symmetrical and therefore, just as there is only one type of scalar, we will have only one basis for the element of maximum degree which will take the name of pseudoscalar, regardless of the dimension ![]() .
.
– in 1D the pseudoscalar is simply ![]()
– in 2D the pseudoscalar is ![]() (=
(= ![]() )
)
– in 3D the pseudoscalar is ![]() (=
(= ![]() )
)
– in 4D the pseudoscalar is ![]() (=
(= ![]() )
)
We have seen that in both 2D and 3D the pseudoscalar squared is -1, but this is not a general rule: for algebras with uniform signature we have the following sequence
| dimension | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 … |
| + | – | – | + | + | – | – | + |
The 2D pseudoscalar anticommutes with vectors and in fact for this reason we do not identify it with the imaginary unit ![]() . In 3D, on the other hand, we verify that it not only commutes with vectors but with all elements. In short, the commutation property of the pseudoscalar depends on both the size of the space and the degree of the element, according to the following table:
. In 3D, on the other hand, we verify that it not only commutes with vectors but with all elements. In short, the commutation property of the pseudoscalar depends on both the size of the space and the degree of the element, according to the following table:
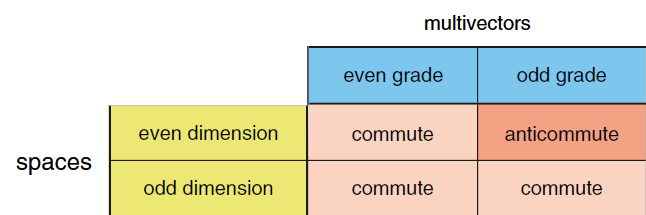
The name pseudoscalar derives from the fact that it behaves like a scalar, that is, it is immune to rotations but undergoes parity transformation (the inversion of all the spatial axes). In 2D and 3D it is transformed into its negative.
Recall some important properties of the pseudoscalar ![]() of
of ![]() :
: ![]()
![]()
![]() for every multivector in
for every multivector in ![]()
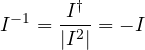
In general, in a ![]() dimension space, if
dimension space, if ![]() then
then ![]()
as we have seen for 2D and 3D ![]() and then the sequence of signs for higher dimensions proceeds alternating in pairs:
and then the sequence of signs for higher dimensions proceeds alternating in pairs: ![]()
