We have said that the multivector M is the linear combination of elements of different degrees:
These four components are distinguished by their behavior with respect to the basic transformations: rotation and inversion of the axes.
The rotation is able to modify vectors and bivectors, but leaves unchanged scalars and pseudoscalars.
The inversion of the axes, on the other hand, is able to change vectors and, since it modifies the sign of the pseudoscalar, it switches the right-hand triple to left-hand, leaving the scalars and bivectors unchanged.
Thanks to these properties, we can build the following table (considering 3D space):
| Affected? | Scalar | Vector | Bivector | Pseudoscalar |
|---|---|---|---|---|
| Inversion | – | yes | – | yes |
| Rotation | – | yes | yes | – |
| Physicsl quantities | energy, mass, length, time, density, electric potential | displacement, velocity, acceleration, electric field | angular velocity, angular acceleration, angular momentum, magnetic field, magnetic dipole, | magnetic flux, helicity |
It is interesting to take a closer look at probably the most elusive component: the pseudoscalar. Now he finally has a physically explorable “suit”. The magnetic flux is the product between the bivector field B and the direction vector; helicity is the projection of the rotation bivector in the direction of the momentum.
It is interesting to note that the Poynting vector, despite originating from a vector product, is NOT a bivector. This is because one of the two factors of the vector product is actually a bivector. And since E and B (intended as vectors) are perpendicular, then E is in the plane of B and therefore the external product 
will have a vector nature and will be perpendicular to E.
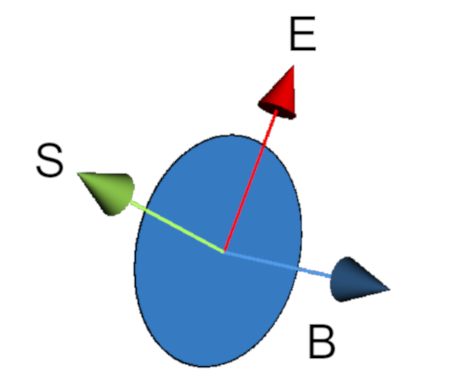
Similarly, the Lorenz force is a vector, despite the fact that it arises from a vector product:
in fact, since 
and B (intended as vectors) are perpendicular, then is in the plane of B and therefore the external product 
it will have a vector nature and will be perpendicular to .
GA also clarifies an obscure aspect of the Lorenz force: why does it manifest perpendicular to speed? In the analogous situation relating to the electric field, the charged particle feels a force directed along the lines of the electric field, while in the case of the magnetic field, it feels a perpendicular force. The answer lies, once again, in the fact that the bivector B is a planar quantity with a direction of rotation, not a small arrow like a vector. This is why the particle feels a force that curves its trajectory.