Intermezzo: numbers generation through the exponential function

Let’s open an extremely fascinating digression, which explains the omnipresence of the exponential function $e^x$ in this discussion. In fact we have determined that the 2D rotation generator is the unit bivector $e_1e_2$ and in fact multiplying it by any vector, it rotates it by $\pi / 2$ .
If we wanted a halved rotation, however, we could not simply multiply it by $e_1e_2 / 2$ . The correct expression goes through the exponential function, which correctly defines the rotor. This is the only way to transfer linearity into the rotation.

Let’s start with a question so simple as to be childish: how are all numbers generated?
The first answer that comes to mind comes from childhood: we learned to count on the fingertips and then the numbers are generated by accumulation from zero step by step. For example, to generate the number 8 we need eight steps.
The second answer is taught to us a few years later, with the multiplication tables. Numbers can be generated by multiplication , imagined as a sequence of addition controlled by a counter.
For example, you get to 8 by accumulating the quantity two for four times, or the quantity four for two times.
At the end of primary school you also learn the concept of power which, analogously, it is a sequence of multiplications of the base controlled by a counter (exponent).

All these ways work, but they always have a kind of algorithm that controls the completion of a process from the outside. We now want to find a process that is as simple and self-explanatory as possible, which springs from itself, without external mechanisms. This process exists and is growth .

Also in the processes we have listed there are some gaps that are difficult to fill.
For example how we explain the expression $10^{1.5} = 2.828 ...$ or the mystical expression $e^{i \pi } + 1 = 0$ or even $i^i = 0.208 ...$ ?

The growth

Let’s start from the philosophical origin of all numbers: the unit.
Now let’s imagine that there is a growth process that in a step of time make the unit to grow by a factor $k$ :

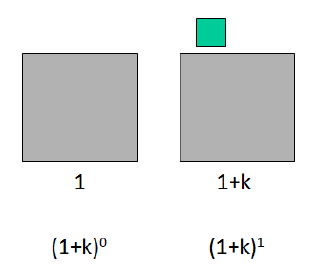
The next step is interesting because it does not only see the generation of another fraction $k$ , indeed another fraction $k^2$ is added, since is coming from the previous grown fraction. This is because in our natural growth all parts are active in the process.

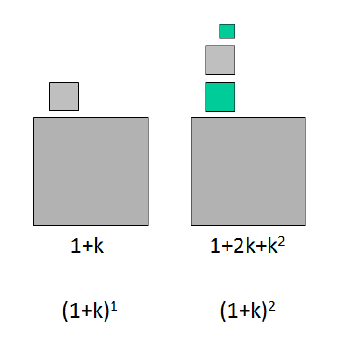
So the third step will see each object generate a k-th fraction of itself

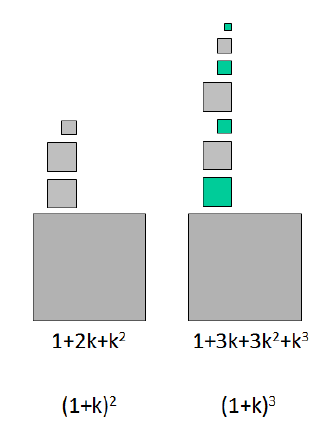
The pattern is now clearly visible:

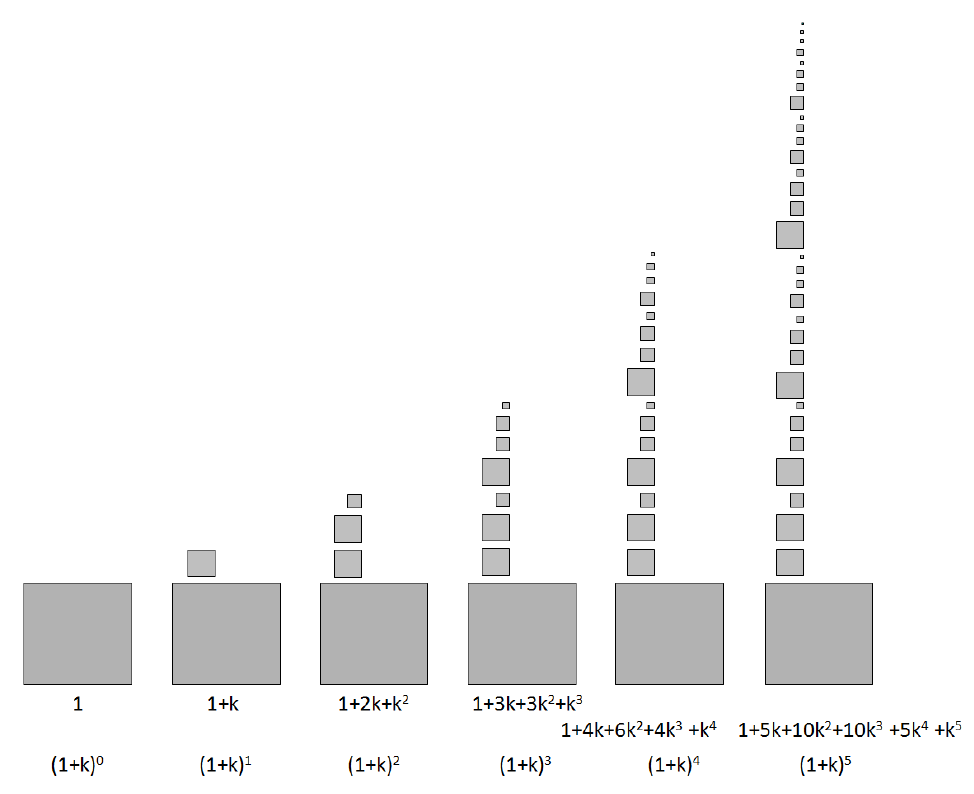
In each step the number of p-elements (those scaled p times, i.e. that measure $k^p$ ) is given by those present in the previous step plus the number of parent elements, i.e. those $p-1$ , according to the Pascal’s triangle:

In fact, we can write each line of Pascal’s triangle as the sum of the previous one and a scaled version of itself.

It is interesting to note that this process is self-similar: the new portion generated at step $k + 1$ is what existed at the previous step scaled by $k$ .

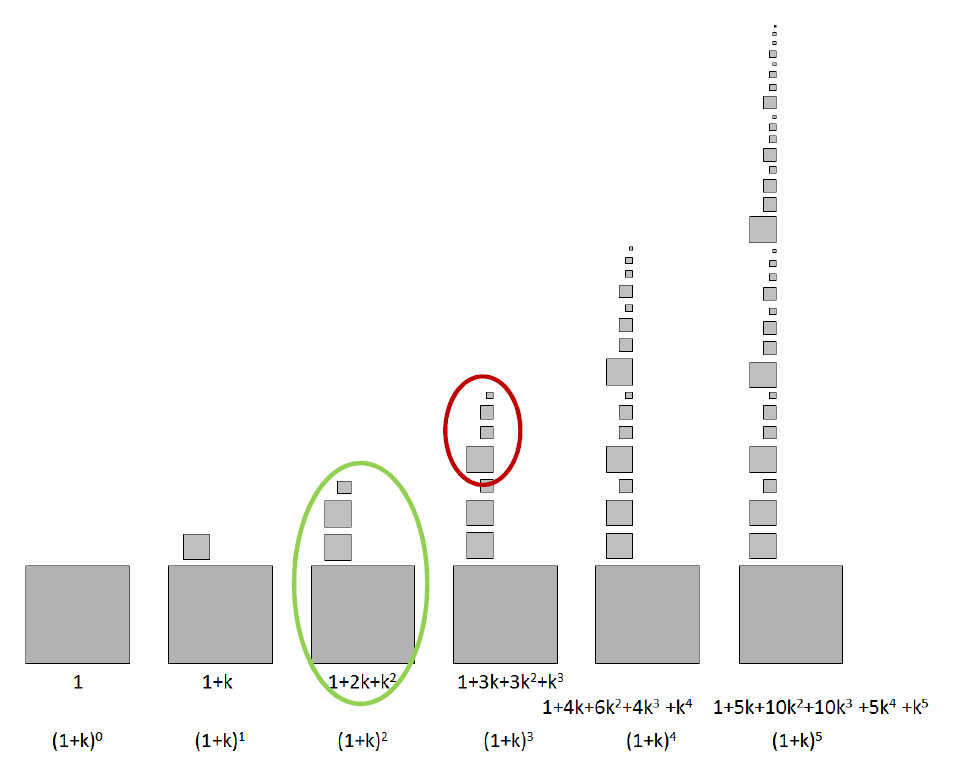
After this premise, let’s get to the heart of the question: we want to explore the property of the natural growth process with k = 1, that is, at each step the quantity generates a copy of itself. We take it as an expression of natural growth because it reminds us of the growth of a tissue by cell division.
If this process took place in a single step, we would have a growth of 1 for a total di 2.
If the process occurs in two steps of size 1/2 then the growth would be proportional to the fraction 1/2 and for the total we can use the expression $(1 + 1/2) ^ 2 = 2.25$
If there were three steps: $(1 + 1/3) ^ 3 = 2.37$
With one hundred steps we would have a good approximation of what continuous natural doubling means:
$(1 + 1/100 ) ^ {100} \approx 2.70$
It is interesting to verify that the limit for an infinite number of steps is a finite quantity and defines one of the most important numbers:

$\begin{equation} \lim_ {n \to \infty} \left (1+ \frac {1} {n} \right) ^ n = 2.7182818 ...$

What if instead of doubling it was a tripling? The expression of the total should be changed like this:

$\begin{equation} \lim_ {n \to \infty} \left (1+ \frac {2} {n} \right) ^ n = 7.37 ... = e ^ 2$

In short, the exponentiation that we learned in elementary schools can be seen as a particular case of a process of continuous growth in which each element generates others, which are an active part in the process. We no longer think of numbers as pebbles to accumulate or divide but rather as a fluid that continuously expands from all its infinitesimal parts .

In summary, our mental model uses three parameters:
– the initial quantity A that we can set to 1, capable of generating all numbers
– the growth factor k, which we can also set to 1 (doubling)
– time, which in effect remains the free parameter

The final amount will be $\text {[initial amount]} \: e^{\text {[growth]} \cdot \text {[time]}}$

For the self-similarity property we talked earlier, each portion of the curve is equal to the curve itself. In particular, since $f (n + 1 / k) = f (n) + f (n) / k$ its derivative is equal to the value of the function itself, being:

$\begin{equation} \lim_ {k \to \infty} \frac {f (n + 1 / k) -f (n)} {1 / k} = f (n)$

Furthermore, it is clear that the value in step $n$ is equal to the sum of all the increments of the previous steps, since for the fundamental theorem of integral calculus:

$\begin{equation} \int_ {0}^n f '(k) dk = f (n) - f (0)$

but we just showed that $f '(x) = f (x)$ and so we have

$\begin{equation} f(n) = f(0) + \int_{0} ^ n f (k) dk$

So we can say that due to the extraordinary function of natural growth, the present coincides with the future (the increase) and with the past (the cumulated value).

We can apply the same reasoning with $k$ being a negative number, which is a continuous erosion of unity. The formula of the final quantity would remain valid and we would obtain that the sequence converges to the value $e^{-k}$ .

Going back to our initial problem of explaining how all numbers are generated, we have obtained a formula that allows us to get all numbers greater than zero, but not zero and not even negative numbers.

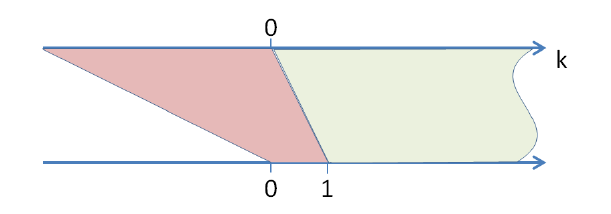
So there remains the problem of naturally generating negative numbers and – while we’re at it – explain why $(- 2)^2 = 4$ and increasing the exponent just by one the whole expression changes sign: $(- 2)^3 = -8$

The imaginary growth

What we have seen can be extended to the imaginary form as follows: the unit grows by an imaginary quantity $ki$ and generates the following sequence:

which we can represent as in the previous case, but with the trick of coloring the imaginary terms in orange, placing them on the left (positive) or on the right (negative). Here too we can notice a quasi self-similarity, because we have to multiply each block of the previous step by $i$ .

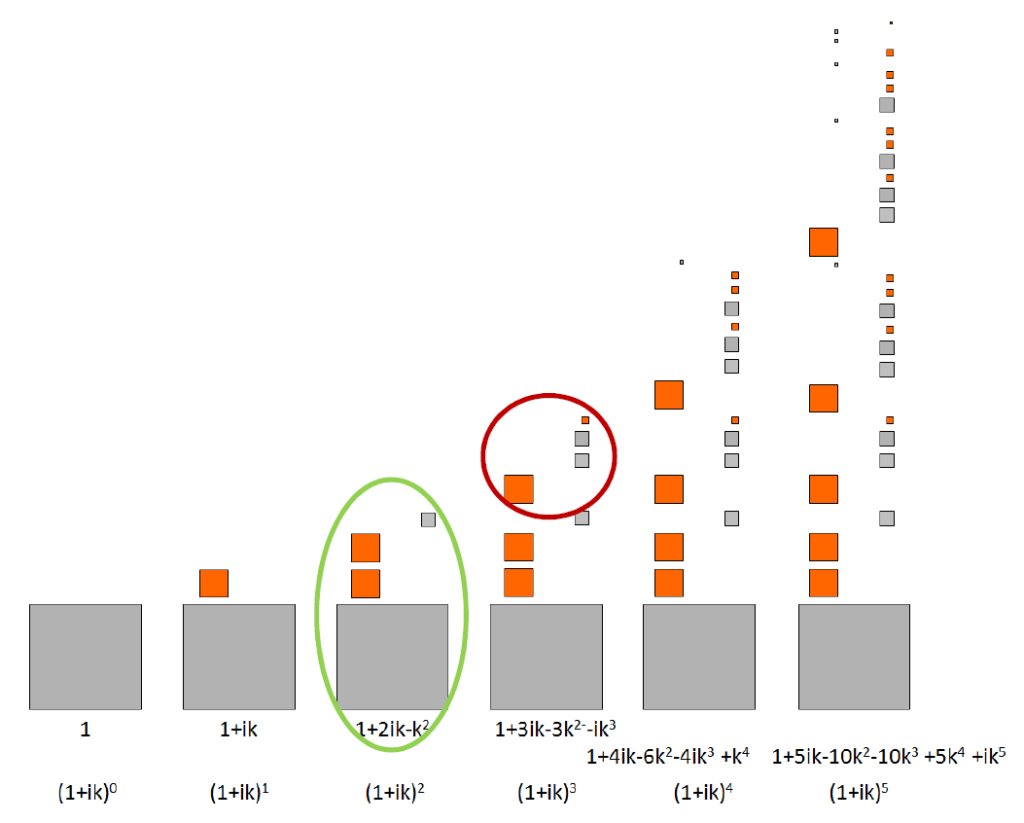
This visualization, however, is too complicated and does not help us: it is better to resort to the Argand-Gauss plane, where the gray and orange squares become the real and imaginary components of a sequence of points.
Let’s say $k = 1/3$ and look at the growth in three steps:

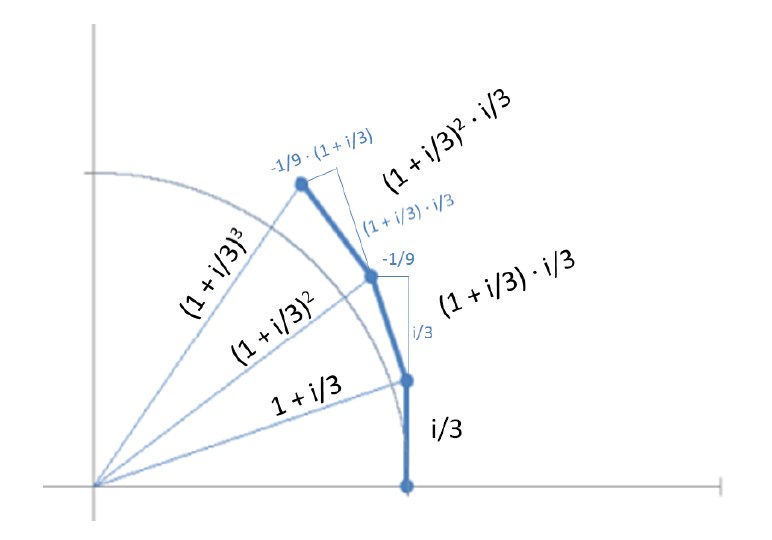
The first step defines a right triangle with major leg 1 and minor leg $i / 3$ their sum is obviously the hypotenuse.
The following steps are linked to the first by the self-similarity relationship, therefore the the second triangle will start from the hypotenuse of the first to which a version of itself scaled by $i / 3$ will be added.
This has an interesting implication: in all steps the angle in the center is the same.

Now imagining to go to the continuous, we increase the steps and observe that the limit of the sequence is on the unit circumference and defines an arc of unit width (in radians).

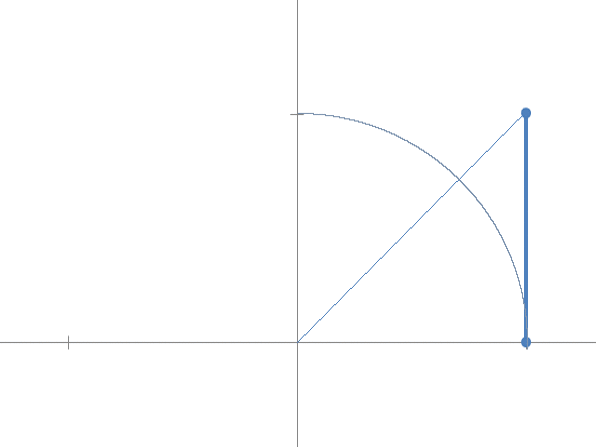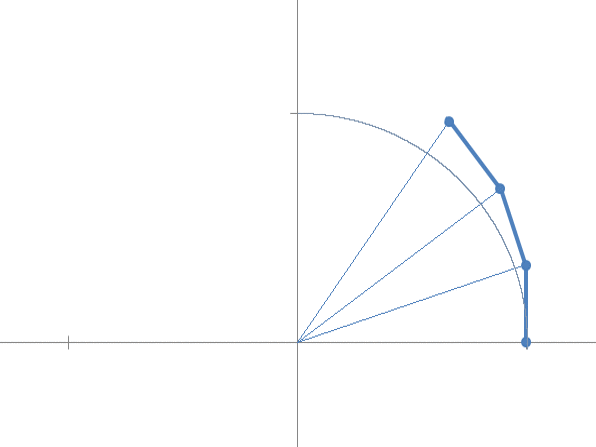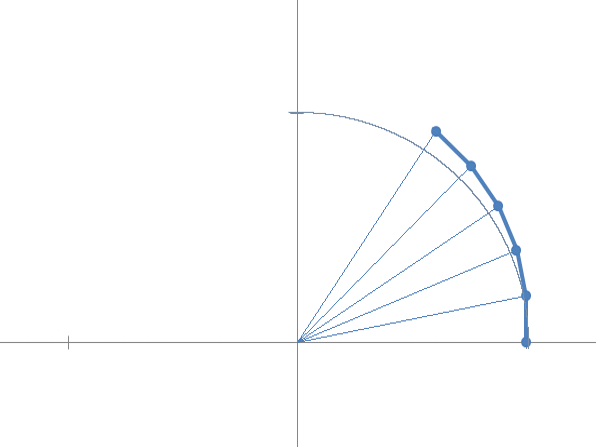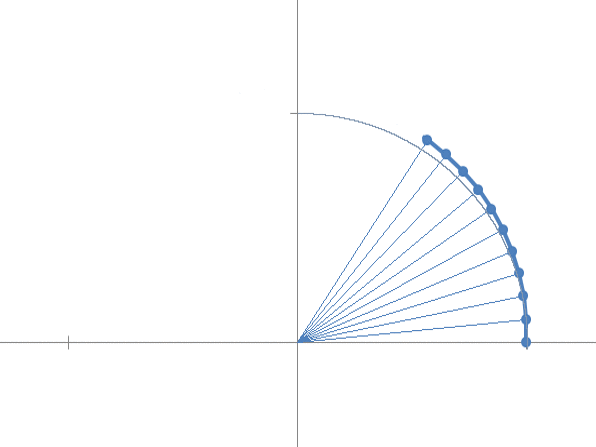
If we now increase the growth factor $k$ , we discover that the sequence converges to a value which is always found on the unit circumference but describing an arc of width 2 radians.

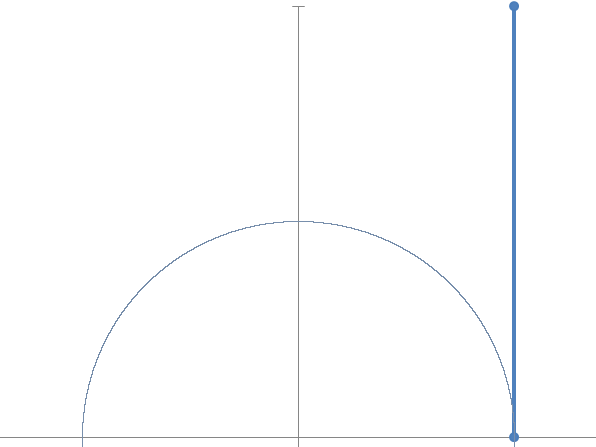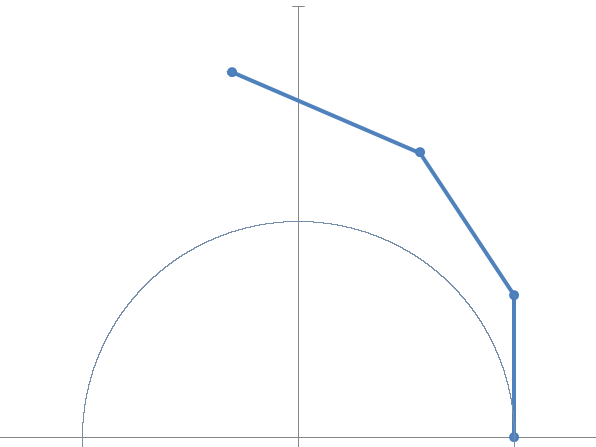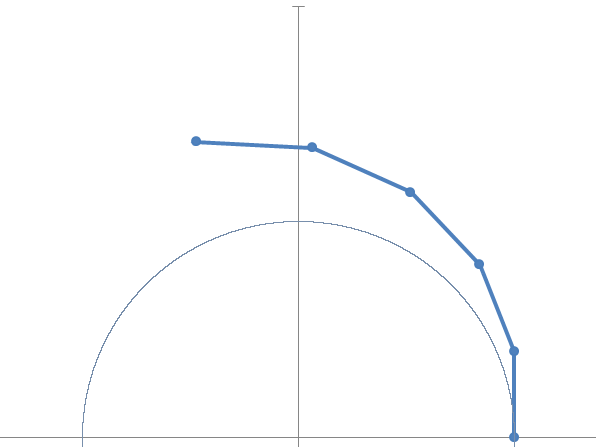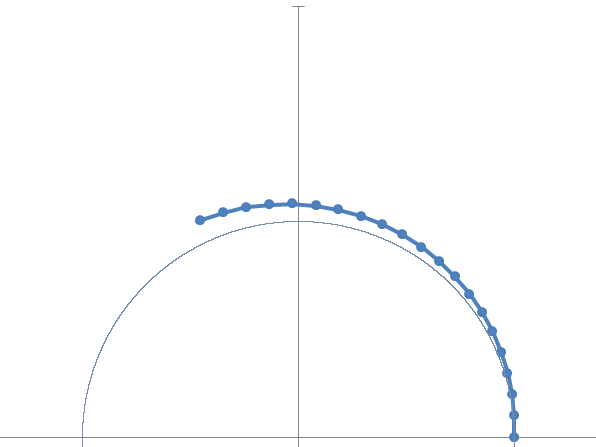
So we can interpret the expression of imaginary growth with the symbolic equivalence:

$\begin{equation} \lim_ {n \to \infty} \left (1+ \frac {ik} {n} \right) ^ n = e^{ik}$

and Euler’s “mystical” formula can be interpreted as the particular case of a process of continuous imaginary growth. If the growth factor is $\pi$ , it causes the number 1 to map to the number -1, that is, to rotate $\pi$ radians.

The synthesis

To summarize, we have found a way to generate all numbers starting from unity in the most natural way possible by means of the same exponential structure $e^x$ .
If $x$ is positive real, it is of a growth, if negative real is a contraction, if it is imaginary it will be a rotation of $x$ radians. By the property of powers, we can combine the two effects in the complex exponent:

$e^a e^{ib} = e^{a + ib}$

which expresses in a single operation the fundamental transformation capable of generating all numbers: scaling and rotating the unit.