Projectile motion – Geometric Algebra

One of the first topics studied in the physics courses is the projectile motion, which has many connections with direct experience: from snowballs to soccer’s penalties. The argument is well suited to summarize the kinematics of an object moving under the influence of a uniform gravitational field, which generates an acceleration $g = 9.81 m/s^2$ .
To solve the exercises correctly you learn the superposition principle, which allows you to separate the motions in the horizontal and vertical directions. Typically the exercises ask to determine the flight time, the range, the final speed and also to calculate the angle of fire that produces the maximum range.

On this page we see everything in the light of geometric algebra.
The situation is the classic one: a projectile is fired with an initial velocity represented by the vector $v_0$ which forms an angle $\theta$ with respect to the horizontal. The position of the bullet at any instant is given by the vector $r$ .

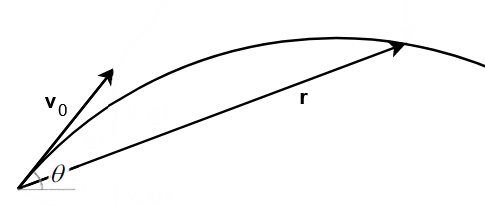
The decisive step is given by the representation of the velocity diagram referred to any instant $t$ . We start from the vector $v_0$ and then we remember that the acceleration of gravity $g$ acts in a vertical direction, so from the tip of $v_0$ a vector facing downwards of modulo $gt$ starts. The sum $v_0 + gt$ yields the final velocity vector $v$ . So far we have drawn a very banal triangle.
Now let’s look at the starting point and the one where the bullet is at the considered instant $t$ : we can calculate the average velocity and this must be equal to the total displacement $r$ divided by the total time $t$ , therefore:

$\begin{equation} \frac{v_0 + v}{2} = \frac{r}{t}$
that is to say
$\begin{equation} v_0 + v = \frac{2r}{t}$

Our construction has been enriched by the sum of $v_0$ and $v$ , forming a parallelogram valid for all instants of motion :

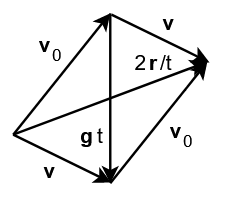
Note that it is sufficient to vary $v_0$ and the parallelogram of the velocities will change accordingly. For example (exercises left to the reader) we can find the classic cases of the free fall or of an object thrown vertically upwards with initial speed $v_0$ .
We will see that to solve all the problems of the motion of the projectiles it is sufficient to solve this elementary parallelogram.

First the simple case: the target to hit is at the same altitude as the starting point. In this particular case, the parallelogram must have the shortest diagonal, which corresponds to the position vector $r$ lying on the horizontal.

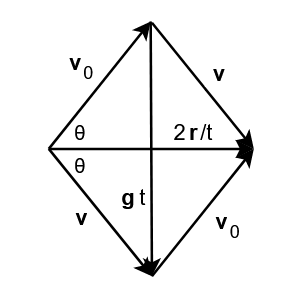
We observe purely geometrically that the vectors $v_0$ and $v$ are equal in magnitude and symmetrical with respect to the horizontal. Let’s now see the calculations, recalling the two properties we built earlier:

$v = v_0 + gt$
$v - v_0 = gt$

and

$v + v_0 = 2r / t$

Let’s multiply them, to eliminate $t$ , remembering that we are in a non-commutative world (i.e. the two terms $- vv_0 + v_0v$ don’t cancel out!):

$(v + v_0)(v - v_0) = 2rg$

$v^2 - vv_0 + v_0v - v_0^2 = 2rg$

let’s recall the very useful identity that we have seen when dealing with the geometric product with regard to the external product: $a \wedge b = (ab - ba) / 2$
Let us also remember that the multiplication of vectors $r$ and $g$ shall be performed using the geometric product.

$v^2 - v_0^2 + 2 (v \wedge v_0) = 2 (r \cdot g + r \wedge g)$

by equating terms of equal degree (scalars with scalars and bivectors with bivectors) we will have:

$v^2 - v_0^2 = 2 \: r \cdot g$

$2 (v \wedge v_0) = 2 \: (r \wedge g)$

But the way we built the problem $r \cdot g = 0$ because they are perpendicular, so the first equation gives us an interesting result: $v^2 = v_0^2$ (it will have something to do with the conservation of energy?).
The second equation concerns the areas (obviously, being bivectors!) but we know how to calculate them easily: if in modulo $v_0 = v$ then the area of the parallelogram is worth $v_0^2 \sin 2 \theta$ and then we can finally write:

$v_0^2 \sin 2\theta = rg$

and therefore the range is

$\begin{equation} r = \frac{v_0^2 \sin 2\theta}{g}$

hence the consideration that, with the same initial speed, the maximum range is for $\theta = \pi / 4$ .

Now let’s complicate things: the target to hit is at a different altitude, let’s say it is higher than the shooting point. Our parallelogram, designed for the starting and ending points of the trajectory, will be the following:

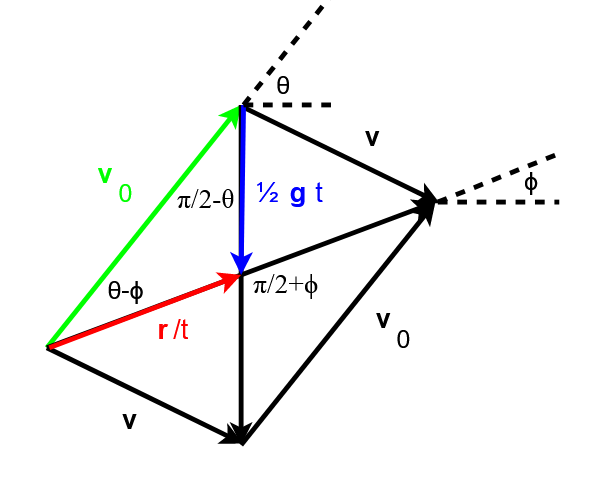
Again we have the shooting angle $\theta$ and the new angle $\phi$ which represents the angle of elevation of the target seen from the start. Note that – in accordance with the geometry of the parallelogram – the diagonals mutually cut in half and therefore the red and blue vectors are respectively worth $r / t$ and $gt / 2$ .

The power of AG is expressed in very elementary ways and makes us feel firsthand that physics is geometry .
By concentrating on the colored triangle, we can see it as half of a parallelogram and have fun determining its area with the three external products between the colored vectors. We will only have to pay attention to:
1) start the vectors from the same point
2) to the direction of the resulting bivector (positive counterclockwise)
like this:

$\begin{equation} \frac{r}{t} \wedge v_0 = \frac{gt}{2} \wedge \frac{r}{t} = \frac{gt}{2} \wedge v_0$

If it were not clear, the second and third wedges are imagined as follows:

Well, after this first step, let’s apply another very important principle of GA: the fact that the product of two versors is a rotor. Looking again at the parallelogram with the rotor eyes, then removing the scale factors of the vectors involved, we can write these equalities:

$\hat{\pmb{r}}\: \hat{\pmb{v}} = e^{i (\theta - \phi)}$

$\hat{\pmb{g}}\: \hat{\pmb{r}} = e^{i (\pi/2 + \phi)}$

$\hat{\pmb{g}}\: \hat{\pmb{v}} = e^{i (\pi/2 + \theta)}$

Now we remember the beautiful expression seen in the rotors’ page:

$e^{i \theta} = \cos \theta + i \sin \theta = a \cdot b + i\: a \wedge b$

and therefore we can say that

$\hat{\pmb{r}}\: \hat{\pmb{v}} = e^{i (\theta - \phi)} \implies \hat{\pmb{r}} \wedge \hat{\pmb{v}} = i\: \sin (\theta - \phi)$

$\hat{\pmb{g}}\: \hat{\pmb{r}} = e^{i (\pi/2 + \phi)} \implies \hat{\pmb{g}} \wedge \hat{\pmb{r}} = i\: \cos \phi$

$\hat{\pmb{g}}\: \hat{\pmb{v}} = e^{i (\pi/2 + \theta)} \implies \hat{\pmb{g}} \wedge \hat{\pmb{v}} = i\: \cos \theta$

Let’s stop and think about these equations. The imaginary unit appears for the first time in our calculations, but we have learned not to be alarmed because now – thanks to the GA – we see it as a geometric entity. The imaginary unit $i$ is a unitary portion of the plane in which our construction lies, and is positively oriented counterclockwise. Nothing more than that.
If $i$ is the pie, $i \: \sin (\theta - \phi)$ is an (oriented) slice of this pie.

Now we really have all the ingredients for our calculations.
Let’s rewrite the equalities between the external products so that the versors are highlighted:

$\begin{equation} \frac{v_0 r}{t}\: \hat{\pmb{r}} \wedge \hat{\pmb{v_0}} = \frac{gr}{2}\: \hat{\pmb{g}} \wedge \hat{\pmb{r}} = \frac{v_0gt}{2}\: \hat{\pmb{g}} \wedge \hat{\pmb{v_0}}$

Then we easily get the flight time from the first two expressions:

$\begin{equation} t = \frac{2v_0}{g} \frac{\hat{\pmb{r}} \wedge \hat{\pmb{v_0}}}{\hat{\pmb{g}} \wedge \hat{\pmb{r}}} = \frac{2v_0}{g} \frac{\sin(\theta - \phi)}{\cos \phi}$

and from the last two, now that we know $t$ , we can get the distance $r$ :

$\begin{equation} r = v_0t\:\frac{\hat{\pmb{g}} \wedge \hat{\pmb{v_0}}}{\hat{\pmb{g}} \wedge \hat{\pmb{r}}} = \frac{2v_0^2}{g}\:\frac{\hat{\pmb{r}} \wedge \hat{\pmb{v_0}}}{\hat{\pmb{g}} \wedge \hat{\pmb{r}}}\:\frac{\hat{\pmb{g}} \wedge \hat{\pmb{v_0}}}{\hat{\pmb{g}} \wedge \hat{\pmb{r}}} = \frac{2v_0^2}{g}\: \frac{\sin(\theta - \phi) \cos \theta}{\cos^2 \phi}$

Note that this result, with the classical technique in rectangular coordinates (American Journal of Physics 47, 466), requires much more complex calculations.

Incidentally, we note that we can recall one of the results obtained for the initial case:

$v^2 - v_0^2 = 2 \: r \cdot g = - 2gh$

and we recognize in this expression the principle of conservation of energy, namely that the loss of kinetic energy is equal to the increase in the potential energy of the projectile.

The meaning of all this, beyond the final formulas, is: physics is essentially geometry and geometric algebra makes things much simpler .

Leave a Reply Cancel reply