3D geometric algebra – Geometric Algebra

In 3D shows up the new base $e_3$ and then if we evaluate all the combinations as already done in the 2D case, we will get:

$M = a + \underbrace{v_1e_1 + v_2e_2 + v_3e_3}_\text{vector} + \underbrace{b_1e_1e_2 + b_2e_2e_3 + b_3 e_3e_1}_\text{bivector} + c \: e_1e_1e_3$

In three dimensions, geometric algebra is generated by 8 bases:

Questa immagine ha l'attributo alt vuoto; il nome del file è 3D-1.png

It will not be overlooked that for each additional dimension the bases are doubled and their distribution by degree follows the row $n-1$ of Pascal’s triangle.
Compared to the 2D world we now have two other basic bivectors and all three have the remarkable property:

$(e_1e_2)^2 = (e_2e_3)^2 = (e_3e_1)^2 = -1$

but also the trivector: $(e_1e_2e_3)^2 = e_1e_2e_3e_1e_2e_3 = -1$ so we can say that bivectors and trivectors are isomorphic to the imaginary unit $i$ . It should not be taken as an absolute property: the pseudoscalar sign derives from the number of dimensions and the signature of the bases. For example, in four dimensions the pseudoscalar squared is +1, but if we are talking about spacetime, then with one of the bases squared to -1, the pseudovector will square to -1.

The trivector

The new element in 3D geometric algebra is defined trivector and can be geometrically interpreted as an oriented volume element. The orientation of a volume is given by the chirality of the basis of trivectors defining it. By convention we will say that it is positive for a right-handed triad.
The following figure should not be taken too literally: just like for the bivector, the information carried by a trivector is an extension, an orientation but NOT a shape.

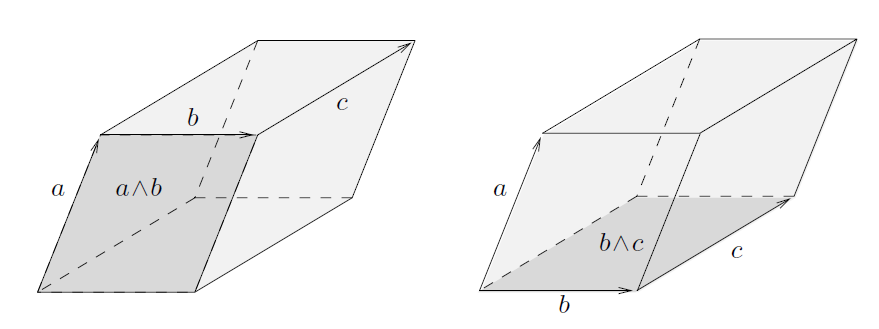
Questa immagine ha l'attributo alt vuoto; il nome del file è trivector.png

The trivector in the figure is generated by the right-handed triad $a \wedge b \wedge c$ and it is sufficient for a single vector to invert for the entire trivector to change sign. Two reversals, however, leave it unchanged.
Since the trivector is the element of the highest degree, in this geometry it takes the role of pseudoscalar, which in 2D was reserved for the bivector.

Pseudovectors

What happens in 3D if we multiply a vector by the pseudoscalar?
Remembering what happens in 2D, we would be tempted to think of a $\pi / 2$ rotation, but the GA is subtle: at first glance it all seems easy, but when one thinks they understand, the correct answer turns out to be a lot richer than you imagined.
Better then to proceed under the safe guidance of equations.
If we multiply the bases of the bivectors with the pseudoscalar $I = e_1e_2e_3$ we get:

$I e_1 = e_2e_3 = e_1I$
$I e_2 = e_3e_1 = e_2I$
$I e_3 = e_1e_2 = e_3I$

this operation does not rotate the vectors, but changes them in the planes perpendicular to them.
So what happens in 2D can be interpreted as a rejection , that is: multiplying a vector by the pseudoscalar projects it into the perpendicular subspace!
If this interpretation holds, then if this time we multiply the bivector $e_1 \wedge e_2$ by the pseudoscaling $I$ we should get the vector $e_3$ and indeed it is (regardless the sign)!
This operation is called duality transformation.
This allows you to rewrite the bivectors in the general expression of the multivector as $I (b_1e_3 + b_2e_1 + b_3e_2)$ and therefore:

$M = a + \underbrace{v_1e_1 + v_2e_2 + v_3e_3}_\text {vector} + \underbrace{I (b_1e_3 + b_2e_1 + b_3 e_2 )}_\text {pseudovector} + c I$

The 3D even sub-algebra: the quaternions

Similarly to when seen in 2D, also in 3D we can identify an even subalgebra, consisting of elements of even degree: scalars and bivectors. It is actually a subalgebra because by multiplying or adding these elements, we always obtain multivectors of even degree (closure):

$M = a + b_1e_1e_2 + b_2e_2e_3 + b_3 e_3e_1$

… if anyone had doubts, the odd degree elements DO NOT constitute a subalgebra, in fact $e_1e_1 = 1$

The even subalgebra in 3D is isomorphic to quaternions, entities introduced by Hamilton in 1843 as extensions of complex numbers to three-dimensional space. It is worth pausing a bit, to illustrate the clamorous misunderstanding has prevented a greater diffusion of quaternions in the scientific world.

The quaternions

Summarizing all the possible products of the elements in 3D:

Questa immagine ha l'attributo alt vuoto; il nome del file è recap.png