(re)starting from scratch – Geometric Algebra

In chemistry the game of Aufbau (construction) allows to obtain the configuration of the orbitals of an atom by progressively adding electrons, according to the energetic sequence of the orbitals. This way it is possible to build the whole periodic table of elements.

In a similar way, let’s try to construct the entire 3D space geometrically starting from the basic elements, with very few rules of absolute reasonableness.
We will therefore start from the basic entity par excellence, the point, imagined without geometric extension.
Two non-coincident points A and B identify an entity that has dimension one and we can imagine that it is generated by extension , i.e. by dragging A towards B. This entity is called a vector (from the Latin veho = to transport, travel, go) and the name itself reveals the idea of transport at the base of its construction.
The extension operation instead we will call it external product or wedge and will be indicated with the symbol ⋀ .
It is not unreasonable to say that if we move B towards A a vector of equal direction and length will be generated, but in the opposite direction, so we can certainly write that:

$\vec{v} &=& A\wedge B &=& - B\wedge A$

So it is important to note that the wedge operation is not commutative, indeed, it is antisymmetric !

Just to show that wedge is well-behaved, we note its properties:

(\lambda a) \wedge b = \lambda(a \wedge b)

\lambda(a \wedge b) = (a \wedge b) \lambda

Continuing in our Aufbau, after having constructed vectors, we can take two non-aligned vectors $\pmb{a}$ and $\pmb{b}$ and imagine that the entity of dimension 2 is generated by extension of $\pmb{a}$ sliding along the vector $\pmb{b}$ .
To this entity we give the name of bivector and, in the same way, it is reasonable to think that this area is oriented, because if it is generated in the opposite way, that is by sliding $\pmb{b}$ along the vector $\pmb{a}$ , it will sweep the same area, but in the opposite direction, as can be seen from the circulation induced by the vectors.

bivector is a signed quantity because the area is

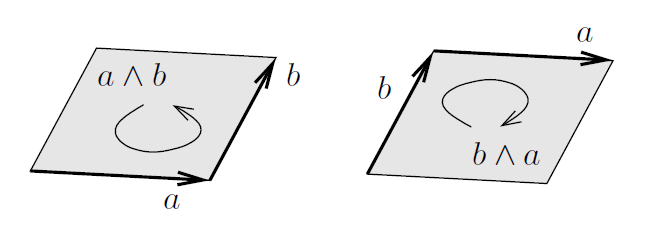
It seems weird, but the bivector has no definite shape: it has only a position, an extension and an orientation. Some people are representing them as circles, others as rectangles. Still others leave the representation consistent with the external product, that is, the parallelogram.

By now the Aufbau is unstoppable: another vector independent from $\pmb{a}$ and $\pmb{b}$ , i.e. outside the plane identified by them, is able to generate by extension a volume by scrolling of the plane along R. Also in this case the volume (called trivector) has a sign: by convention it is positive if the triad is right-handed. As with bivectors, trivectors also have no definite shape.

Geometric algebra, therefore, sees as basic elements not only vectors, but also areas and volumes.
Now let’s add some algebra to the geometric intuition.

The bases of ordinary vectors are the $e_1$ , $e_2$ , $e_3$ vectors for which the following fundamental property holds (it is the real heart of geometric algebra)

$e_1^2 = e_1e_1 = e_2^2 = e_2e_2 = e_3^2 = e_3e_3 = + 1$

(careful: it’s a matter of definition! also the $-1$ choice is possible, but let’s keep it simple by now)

These bases can be combined linearly with real coefficients and give rise to ordinary vectors, which have degree one:

$\pmb{v} = v_1e_1 + v_2e_2 + v_3e_3$

We can also combine the bases $e_1$ , $e_2$ , $e_3$ , to form three more bases but this time two-dimensional and oriented. Although the choice of a $e_i_j$ rather than a $e_j_i$ is arbitrary, we will denote the bases of 3D bivectors with $e_1e_2, e_2e_3, e_3e_1$ which is easily remembered because the sequence is cyclic. The product between the bases is anticommutative, therefore:

$e_2e_1 = - e_1e_2$
$e_3e_1 = - e_1e_3$
$e_3e_2 = - e_2e_3$

These bases, similarly to vectors, can be combined linearly and give rise to bivectors, which have degree two:

$\pmb{W} = w_1 e_1e_2 + w_2 e_2e_3 + w_3 e_3e_1$

The fact that the product of the bases is anticommutative has a very important consequence: if we try to calculate the square of any bivector, we obtain that:

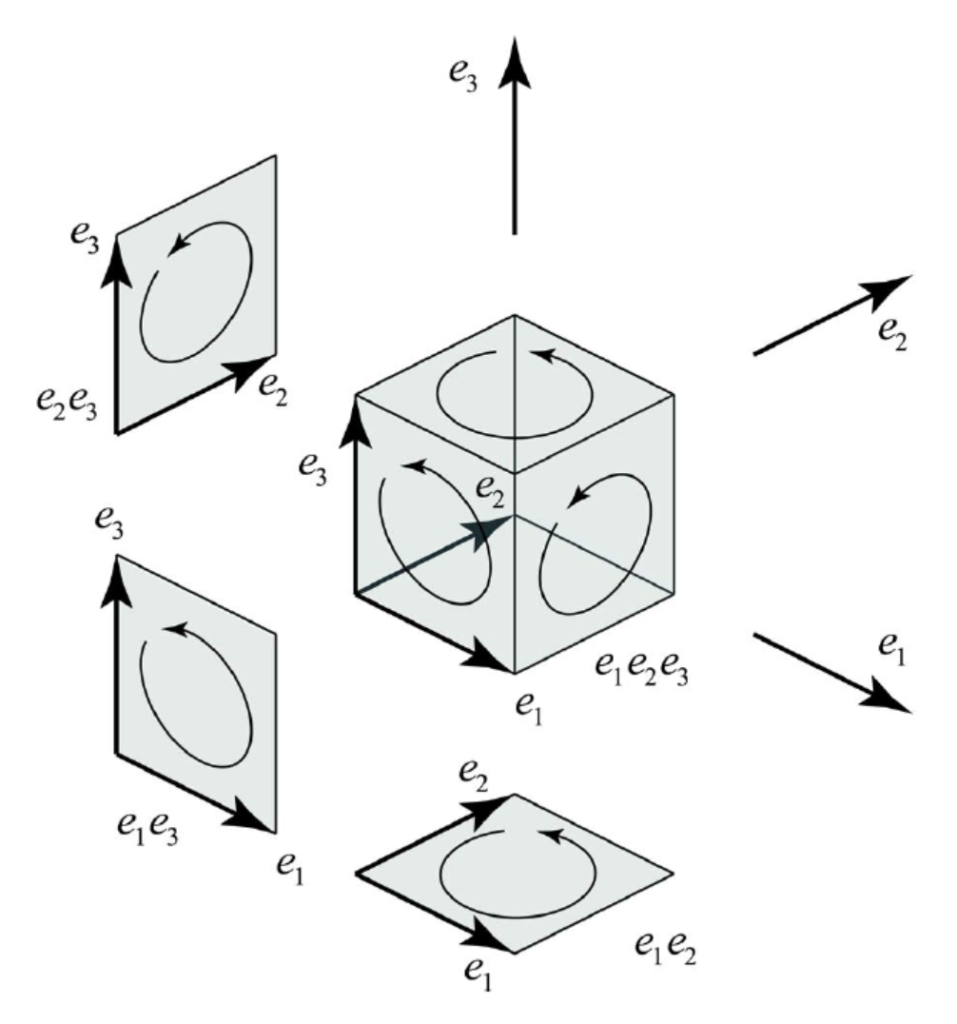
$(e_1e_2)^2 &=& (e_1e_2)(e_1e_2) &=& e_1(e_2e_1)e_2 &=& e_1(-e_1e_2)e_2 &=& -e_1e_1e_2e_2 &=& -1$

3D geometric algebra elements (…actually the scalar is missing!)

Finally, we can combine all three bases together, forming the signed quantity $e_1e_2e_3$ because it is oriented (the one defined by a right-handed triple is positive by convention). This quantity is called the trivector.

As we have already seen for bivectors, if we calculate the square of a trivector, remembering that every exchange of elements involves an inversion of sign, we get:

$(e_1e_2e_3)^2 &=& (e_1e_2e_3)(e_1e_2e_3) &=& -1$

This elegant generalization of the Cartesian space $\mathbb{R}^3$ allows you to directly define and manipulate oriented areas and oriented volumes. Not only that: this algebra includes all linear combinations of scalars, vectors, bivectors and trivectors.

In three-dimensional physical space, therefore, we can define eight-dimensional geometric entities that are called multivectors . They are composed of several elements of different degrees, starting with the scalar, which has zero degree.

$\pmb{M} = \alpha + \underbrace {v_1e_1 + v_2e_2 + v_3e_3} _ \text {vector} + \underbrace {w_1 e_1e_2 + w_2 e_2e_3 + w_3 e_3e_1} _ \text {bivector} + \beta e_1e_2e_3$

The multivector looks like a map of heterogeneous entities that is not allowed to add up. It is actually analogous to complex numbers: it is the sum of several components that form a single entity.

Summarizing:

grade	object	drawn as	geometric extension	algebric extension
0	scalar	point	none	magnitude
1	vector	oriented segment	1-direction	length
2	bivector	oriented area	2-directions	surface
3	trivector	oriented volume	3-directions	volume
…	…	…	…

Exercise: simplify the expression $e_2e_3e_2e_1e_3e_2e_2$

$(\lambda a) \wedge b = \lambda(a \wedge b)$	multiplication by scalar is associative
$\lambda(a \wedge b) = (a \wedge b) \lambda$	multiplication by scalar is commutative
$a \wedge (b+c) = (a \wedge b) + (a \wedge c)$	wedge is distributive with respect to the sum
( $a \wedge b) \wedge c = a \wedge (b \wedge c)$	wedge is associative