Opposite, conjugated, inverse – Geometric Algebra

To adequately complete the description of geometric algebra, next to the Aufbau with which the elements are constructed, it is also necessary to describe the dark side : that is the elements in some opposite mode of a generic multivector $M = a + \pmb{v} + B + bI$ .
This is essential for the correctness of some operations, such as splitting or rotation in the opposite direction.

This page can be boring or interesting. When viewed from the algebraic side, it is undoubtedly boring. On the other hand, when viewed from the geometric side, it is very interesting. The funny thing is that these are the same concepts, which in GA are interpretable in an algebraic or spatial sense, but their root is common.

Opposite

The most elementary negative construct of a multivector is the opposite, which sees all its elements change in sign: $-M = - a - \pmb{v} - B - bI$

Conjugate (reverse)

We define conjugate the multivector $M^\dagger$ ( $\dagger$ is the symbol called dagger or also obelisk) sometimes it is indicated with $M^{\sim}$ in which all the terms that are added in the generic multivector see inverted the order of their factors. Here are some examples:

From the point of view of calculation, it must be remembered that conjugation is a recursive operation: $(ab)^\dagger = b^\dagger a^\dagger$

The conjugation operation obviously leaves scalars and vectors unchanged, while the sign of bivectors and trivectors changes. As you can see, the pattern for the different grades is as follows: + + – – + + – – …

The generic multivector
$M = a + \pmb{v} + B + bI$
is transformed by conjugation in the multivector
$M^\dagger = a + \pmb{v} - B - bI$

Inverse

As far as we have just said,

$A^\dagger A = AA^\dagger = a_n ... a_3 (a_2 (a_1a_1) a_2) a_3 ... a_n =$
$|a_1|^2 (a_n … (a_3 (a_2a_2) a_3) … a_n =$
$= |a_1|^2 + |a_2|^2 + |a_3|^2 + ... + |a_n|^2$

which is a real number, very useful if we want to calculate the inverse of a multivector M, in fact:

$M^{-1} M = 1$
$M^{-1} M M^\dagger = M^\dagger$
and therefore

$\begin{equation} M^{-1}=\frac{M^\dagger}{MM^\dagger} = \frac{M^\dagger}{|M^2|}$

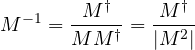
Note that the inverse of a base vector coincides with the base itself: $e_x^{-1} = e_x^\dagger / |e_x|^2 = e_x$

We have said that GA is superior to what is commonly taught because it has a well-made definition of product between vectors, which is also invertible. The inverse of a vector is what multiplied by the vector itself brings it back to unity:

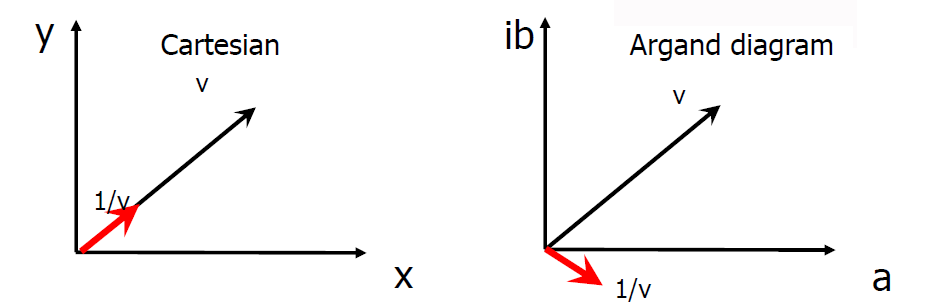
$\begin{equation} \pmb{v}\pmb{v}^{-1}=1=\pmb{v} \frac{\pmb{v}}{|\pmb{v}|^2}$

The most brilliant students will not have escaped this oddity: when we speak of the inverse of a complex number, however, the expression is given by:

$\begin{equation} \frac{1}{z} = \frac{1}{(a+ib)} = \frac{1}{a^2+b^2}(a-ib)$

and we see well that the denominator is the same, but in this case we have the conjugate in the numerator!
Graphically the difference is clear: one more reason to be convinced that complex numbers are something radically different from a vector and therefore should not be confused for any reason.

The inverse of a vector and a complex number show that they are NOT the same geometric object

Exercise: calculation of the inverse of a vector. Let’s take two vectors:

$\pmb{a} = e_1 + 2 e_2$
$\pmb{b} = 3 e_1 + 2 e_2$

Their scalar product is $\pmb{a} \cdot \pmb{b} = a_1b_1 + a_1b_2 = 3 + 4 = 7$
Their wedge is $\pmb{a} \wedge \pmb{b} = -4 e_1e_2$
Their geometric product then is $\pmb{a} \pmb{b} = 7 - 4 e_1e_2$
From the product we can find $\pmb{b}$ knowing $\pmb{a}$ as follows:

$\begin{equation} b = a^{-1}(ab) = \frac{e_1 + 2 e_2}{5} (7 - 4 e_1e_2) = 3 e_1 + 2 e_2$

$M_1 = e_2e_3e_4$	$M_1^ \dagger = e_4e_3e_2$
$M_2 = P+(Q \wedge R)$	$M_2^ \dagger = P + (R \wedge Q)$
$B = \pmb{a} \wedge \pmb{b}$	$B^\dagger = -B$