Vectors vs quaternions – Geometric Algebra

When we discussed the 2D geometric algebra, we realized that bivectors are able to rotate vectors. We are curious to see if it also works in 3D.

Let’s calculate the product between a vector and a bivector: the vector can be decomposed into a component in the plane of the bivector $a_\parallel$ and a perpendicular to it. Since it doesn’t have a shape, we can reshape the bivector so that it turns out to be $F = (a_\parallel \wedge c)$

The product between a vector and a bivector in 3D

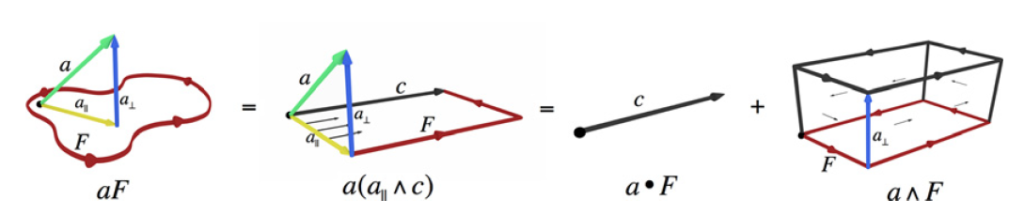
The result will consist of two parts: $a_\parallel F + a_\perp F = | a_\parallel || c | + a_\perp \wedge F$ that is the vector $a_\parallel$ rotated by $\pi / 2$ in the plane of F and the trivector $a \wedge F$ .
So actually the bivector has rotated the component of the vector that lay in its plane, but it has also generated a volume which, due to the rotation we are looking for, remains … indigestible.
If we try to swap the factors, the rotation of $a_\parallel$ reverses, but that bothersome volume is still there.

Without giving us further headaches, the solution has already been stated when we talked about rotors: the sandwich product $BvB^{- 1}$ is what it takes to generate a pure rotation and make the trivector disappear (it cancels out).

$v = v_1 e_1 + v_2 e_2 + v_3 e_3$
$B = w + x e_1e_2 + y e_2e_3 + z e_3e_1$
$B^\dagger = w - x e_1e_2 - y e_2e_3 - z e_3e_1$
con $w^2 + x^2 + y^2 + z^2 = 1$ because

$v' = BvB^\dagger$ rotated by $2 \theta$ in the $B$ plane

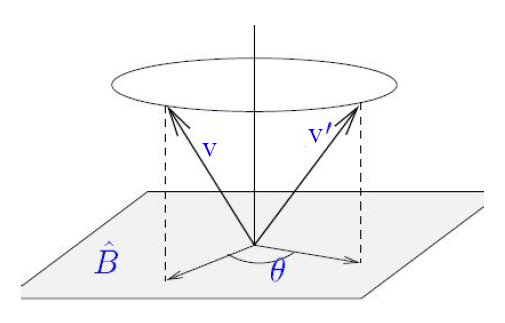
and after long and boring calculations, we will obtain the rotation matrix of the quaternions:

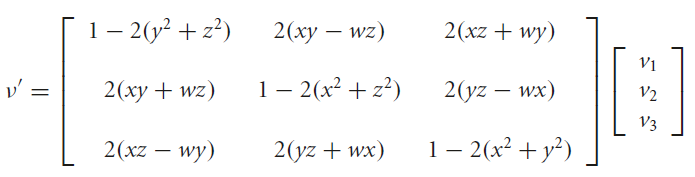
that we will gladly forget, totally relying on the power of the sandwich product!

Rotations in 3D are NOT commutative and this is an important element in favor of the use of GA, which carries non-commutativity in its DNA.
To calculate two successive rotations, then we will proceed as follows:

$v' = BvB^\dagger = exp(-i_1\theta_1/2) \: v \: exp(i_1\theta_1/2)$

represents the first rotation and the second will act on the result of the first, that is:

$v' = CBvB^\dagger C^\dagger = exp(-i_2\theta_2/2)\: exp(-i_1\theta_1/2)\: v \: exp(i_1\theta_1/2)\: exp(i_2\theta_2/2)$

in 3D (and only in 3D) we can identify a single rotation as a result of the two aforementioned:

$\begin{equation} exp(e_1e_2\: \frac{\pi}{4}) \: exp(e_2e_3\: \frac{\pi}{4}) = [\cos \frac{\pi}{4} + e_1e_2 \sin \frac{\pi}{4}][\cos \frac{\pi}{4} + e_2e_3 \sin \frac{\pi}{4}]$
$\begin{equation} = \frac{1}{2} (1 + e_1e_2)(1 + e_2e_3) = \frac{1}{2} + \frac{e_1e_2 + e_2e_3 + e_1e_3}{\sqrt 3} \frac{\sqrt 3}{2}$
$\begin{equation} = \cos \frac{\pi}{3} + \frac{e_1e_2 + e_2e_3 + e_1e_3}{\sqrt 3} \: \sin \frac{\pi}{3}$
$\begin{equation} = exp \left( \frac{e_1e_2 + e_2e_3 + e_1e_3}{\sqrt 3} \: \frac{\pi}{3} \right)$

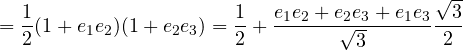
which finally corresponds to a rotation of 120 degrees on a plane that we find it difficult to identify: in fact for our imagination it is much easier to visualize the rotation axis.
To find it we resort to the known duality: $(e_1e_2 + e_2e_3 + e_1e_3)(e_3e_2e_1) = e_1 - e_2 + e_3$