A different angle definition – Geometric Algebra

We have seen one of the most interesting results of geometric algebra: reducing complex numbers to the rotation operation, expressed by means of the rotor $U = e^{- i \theta}$ .
This causes the $e^x$ function to be interpreted differently depending on the type of object represented by the argument.
If the argument is a scalar we will have the ordinary exponential, but if it is a bivector, then we will have a rotation operator. It remains to understand the unit of measurement of this bivector.

In this regard we observe an anomaly: circular functions have an arc as argument (in red), while in hyperbolic ones the argument is double the area highlighted in yellow (the hyperbolic sector).

Circular and hyperbolic goniometric functions are defined with arguments of different type

Let’s try to rethink the concept of rotation: what does it mean to rotate by an angle $\theta$ ? How do we choose it? How do we visualize it?

Typically the angle is the dimensionless unit defined in a circle as the ratio between the arc length and the radius: $\theta = {l} / {r}$ . The round angle is therefore:

$\begin{equation} \theta_{round, linear} = \frac {2 \pi r} {r} = 2 \pi \: \text{radians}$

The radian is precisely the anomalous unit of measurement (actually in the International System it is a pure number) chosen to simplify the expression of the goniometric functions, in particular the important limit:

$\begin{equation} \lim_{\theta \to 0} = \frac {\sin \theta} {\theta} = 1$

from which can be derived equally simple expressions, for example

$\begin{equation} \frac {d}{d\theta} \sin \theta = \cos \theta$

or even their series expansion:

$\begin{equation} \sin \theta = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} ...$
$\begin{equation} \cos \theta = 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} ...$

If there were other definitions of angle, the previous expressions would carry conversion factors and their powers.

In principle we could choose another definition, as long as you leave the argument dimensionless. For example, respecting the bivectoral nature of the $\theta$ angle, we could choose the ratio between the area of the circular sector and the square of the radius:

$\begin{equation} \theta_{full circle, areal} = \frac{\pi r^2}{r^2} = \pi$

This, however, as seen before, would upset all the definitions in use, altering their numerical value! So we propose a small modification: the areal angle is double, therefore:

$\begin{equation} \theta_{areale} = \frac{2 A}{r^2} = 2 \pi$

where A is the area in the figure, which therefore corresponds perfectly to the sector used in the hyperbolic functions.

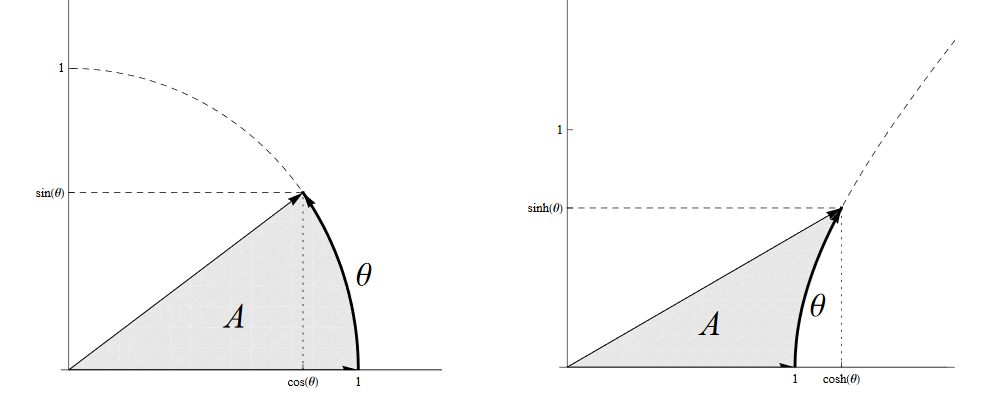
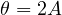
Circular trigonometric functions are defined like this:

$\begin{equation} \cos x = \frac{e^{i \theta }+e^{-i \theta}}{2}$
$\begin{equation} \sin x = \frac{e^{i \theta }-e^{-i \theta}}{2i}$

and they work independently of the interpretation of the angle in a linear or areal way.
As for hyperbolic functions, it would be very nice if they had structurally similar expression:

$\begin{equation} \cosh x = \frac{e^{ \theta }+e^{ -\theta}}{2}$
$\begin{equation} \sinh x = \frac{e^{ \theta }-e^{-\theta}}{2}$

but this happens if and only if the angle is taken as double the hyperbolic sector. In this case we have no choice and frankly it is an interesting coincidence that it also works for the circular counterpart.

For all these reasons, we propose to consider the angles expressed in imaginary units $i \theta$ , since they represent a rotation of defined amplitude $\theta$ in a plane defined as $i$ . The arc instead is represented by the expression $e^{i \theta}$ as explained on this page.
This clarifies the anomaly of radian and steradian which are counted among the derived units of the International System, in the sense that they have one well-defined status and cannot be added to other pure numbers, yet they have no units of measurement.

Leave a Reply Cancel reply