Una diversa interpretazione dell’angolo

Abbiamo visto uno dei più interessanti risultati dell’algebra geometrica: ricondurre i numeri complessi all’operazione di rotazione, espressa per mezzo del rotore $U = e^{−i\theta}$ . Questo fa sì che la funzione $e^x$ sia interpretata diversamente a seconda del tipo di oggetto rappresentato dall’incognita. Se si tratta di uno scalare avremo l’ordinaria esponenziale, ma se si tratta di un bivettore, allora avremo un operatore di rotazione. Resta da capire l’unità di misura di questo bivettore.

A questo proposito osserviamo un’asimmetria: nelle funzioni circolari l’argomento è naturalmente un arco (in rosso), mentre in quelle iperboliche è il doppio dell’area del settore (in giallo). La ragione è profonda: sul cerchio l’arco di lunghezza θ e il doppio dell’area del settore danno lo stesso numero, e possiamo usare indifferentemente l’uno o l’altro. Sull’iperbole questa libertà non c’è — la lunghezza dell’arco iperbolico non coincide con il parametro che genera le funzioni, e l’unico “ponte” naturale resta l’area. È quindi l’area, non l’arco, la nozione che funziona in entrambi i casi.

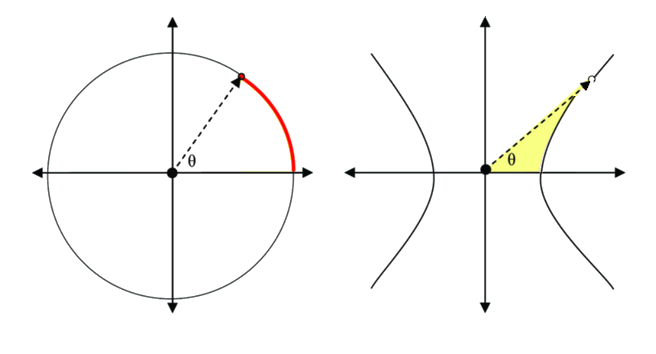
Le funzioni goniometriche circolari e iperboliche sono definite con argomenti di tipo diverso

Proviamo a ripensare il concetto di rotazione: che significa ruotare di un angolo θ? Come lo scegliamo? Come lo visualizziamo?

Tipicamente l’angolo è la quantità adimensionale definita in un cerchio come il rapporto tra la lunghezza dell’arco e il raggio: θ = l/r. L’angolo giro vale dunque:

$\begin{equation} \theta_{giro, lineare} = \frac{2 \pi r}{r} = 2 \pi \: \text{radianti}$

Il radiante è l’unità scelta per semplificare l’espressione delle funzioni goniometriche, in particolare del limite notevole:

$\begin{equation} \lim_{\theta \to 0} \frac{\sin \theta}{\theta} = 1$

dal quale derivano poi espressioni altrettanto semplici, ad esempio

$\begin{equation} \frac {d}{d\theta} \sin \theta = \cos \theta$

o anche la loro espansione in serie:

$\begin{equation} \sin \theta = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} \ldots$

$\begin{equation} \cos \theta = 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} \ldots$

Se ci fossero altre definizioni di angolo, le espressioni precedenti si porterebbero dietro fattori di conversione e le loro potenze.

In linea di principio possiamo scegliere una definizione qualsiasi, purché lasci l’argomento adimensionale. Proviamo allora a misurare l’angolo tramite l’area del settore invece che tramite l’arco. Non si tratta di un’unità diversa: per ogni settore circolare vale l’identità A = ½ r²θ, da cui

$\begin{equation} \theta = \frac {2A}{r^2}$

Il fattore 2 non è un aggiustamento arbitrario — è esattamente ciò che compare nella formula dell’area del settore. Di conseguenza l’angolo “areale” così definito coincide sempre, e non solo sull’angolo giro, con il consueto angolo “lineare” arco/raggio:

$\begin{equation} \theta_{areale} = \frac{2 A}{r^2} = 2 \pi \text{(sull'angolo giro)}$

Cambia l’interpretazione geometrica (un’area orientata anziché un arco), non il valore numerico. E, cosa notevole, questa stessa quantità — il doppio dell’area del settore — è proprio l’argomento utilizzato nelle funzioni iperboliche.

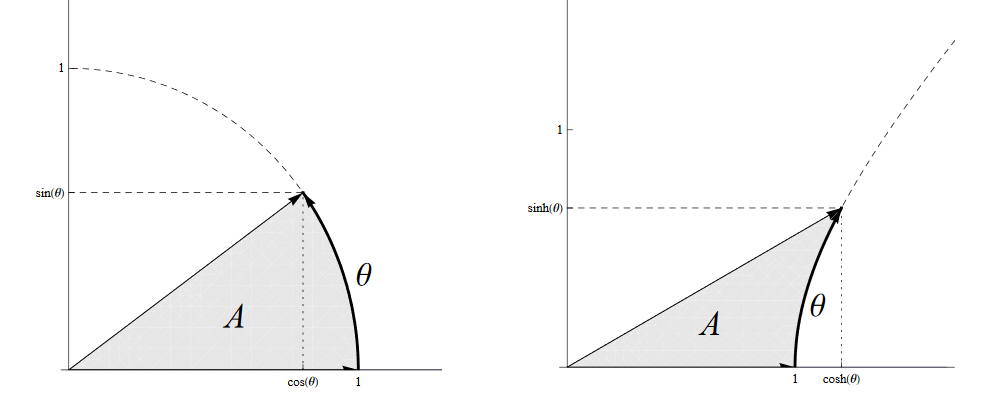
Per entrambe le situazioni, $\theta = 2A$

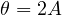
Le funzioni trigonometriche circolari sono definite così:

$\begin{equation} \cos x = \frac{e^{i \theta }+e^{-i \theta}}{2}$
$\begin{equation} \sin x = \frac{e^{i \theta }-e^{-i \theta}}{2i}$

e funzionano indipendentemente dall’interpretazione dell’angolo in modo lineare o areale. Le funzioni iperboliche, dal canto loro, assumono la forma strutturalmente simmetrica

$\begin{equation} \cosh x = \frac{e^{ \theta }+e^{ -\theta}}{2}$
$\begin{equation} \sinh x = \frac{e^{ \theta }-e^{-\theta}}{2}$

se e solo se l’argomento è il doppio dell’area del settore iperbolico. Che lo stesso valga per la controparte circolare non è una coincidenza: discende dalla medesima identità (cos²θ + sin²θ = 1 sul cerchio, cosh²θ − sinh²θ = 1 sull’iperbole), che in algebra geometrica è una sola e stessa relazione. È proprio questa unità di fondo tra cerchio e iperbole il punto centrale.

Per tutti questi motivi, avanziamo sommessamente la proposta di abbandonare il fuorviante concetto di “unità immaginaria” e di considerare gli angoli espressi direttamente come quantità bivettoriali Iθ. Essi rappresentano a tutti gli effetti una rotazione di ampiezza θ all’interno di un piano reale e orientato, definito proprio dal bivettore unitario I (in 2D, il bivettore e₁e₂).

L’espressione $e^{I\theta}$ agisce quindi come operatore di rotazione nel piano: applicata a un vettore lo fa scorrere lungo la circonferenza, individuando l’estremo dell’arco (come spiegato in questa pagina). (Nota tecnica: in 2D la moltiplicazione per $e^{I\theta}$ è già una rotazione. Nel formalismo completo valido in tre o più dimensioni, invece, la rotazione si esprime come “sandwich” col rotore di semiangolo, $v \mapsto e^-{I\theta/2} v e^+{I\theta/2}$ , dove i due fattori compaiono con segno opposto; l’essenza geometrica del processo rimane invariata. In dimensione tre il piano di rotazione resta individuato da un bivettore I e non va confuso con lo pseudoscalare e₁e₂e₃.)

Questo approccio chiarisce un disagio storico attorno a radiante e steradiante: il Sistema Internazionale li classifica come unità derivate adimensionali, eppure un angolo “porta con sé” un’informazione che il puro numero perde — non a caso non lo si somma a un conteggio di mele o a un fattore di scala. La lettura bivettoriale rende finalmente esplicito quel “qualcosa”: la giacitura e l’orientazione del piano $I$ in cui avviene la rotazione. Da qui la proposta di scrivere gli angoli in modo geometricamente completo, come $I\theta$ .