L’algebra geometrica 2D – Algebra geometrica

In due dimensioni l’algebra geometrica, indicata come $\mathbb{G}_2$ o anche $Cl_2$ in quanto basata sulla teoria delle algebre di Clifford, è generata dalle basi $e_1$ ed $e_2$ che si combinano per contrazione ed estensione, ovvero per prodotto scalare e prodotto esterno.

$e_1 e_1 = e_1 \cdot e_1 + e_1 \wedge e_1 = 1 + 0 = 1$ (scalare)
$e_1 e_2 = e_1 \cdot e_2 + e_1 \wedge e_2 = 0 + e_1_2$ (bivettore)

dato che l’algebra geometrica NON è commutativa, vale la pena anche calcolare:

$e_2 e_1 = e_2 \cdot e_1 + e_2 \wedge e_1 = 0 + e_2_1 = - e_1e_2$ (bivettore opposto)
$e_1_2 e_1 = -e_2$
$e_1_2 e_2= e_1$

ed il prodotto più interessante di tutti:

$e_1_2 e_1_2 = e_1e_2e_1e_2 = -1$

Diciamo interessante perché ci mostra due cose:

il quadrato del bivettore vale 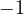$-1$ e pertanto può essere assimilato all’unità immaginaria 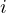$i$ , anche se per cautela lo indicheremo con un simbolo diverso: 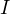$I$ maiuscolo
l’algebra geometrica 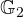$\mathbb{G}_2$ è chiusa, cioè il tentativo di estendere gli elementi di grado 2 mediante prodotto esterno porta al collasso in gradi inferiori

Riassumendo, in due dimensioni l’algebra geometrica è formata dalle seguenti basi:

che concorrono a formare il multivettore

$M = a + \underbrace{v_1e_1 + v_2e_2}_\text{vector} + b_1e_1e_2$

La sottoalgebra pari: i numeri complessi generalizzati

E’ interessante notare che in $G_2$ possiamo vedere una sottoalgebra pari, formata dagli elementi di grado pari (scalari e bivettori). E’ sottoalgebra perché gli elementi di grado pari sono un insieme chiuso rispetto a somma e moltiplicazione.

I ben noti vettori e la sottoalgebra pari, che abbiamo chiamato numeri complessi generalizzati, sono due sottoinsiemi dell’algebra geometrica 2D. Scopriamo quali interazioni esistono fra questi due mondi.