Nel biennio della scuola superiore vengono presentate le equazioni di secondo grado e la formula per la loro soluzione, pur limitando il trattamento alle soluzioni reali.
Vogliamo qui presentare un metodo generale di risoluzione grafica di tutte le equazioni di secondo grado, anche quelle con ![]() utilizzando un’app realizzata in geogebra. Lo scopo è mostrare quanto utilmente i due mondi della traslazione e della rotazione sono complementari.
utilizzando un’app realizzata in geogebra. Lo scopo è mostrare quanto utilmente i due mondi della traslazione e della rotazione sono complementari.
Clicca per aprire l’app Geogebra
Partiamo dalla classica equazione di secondo grado ![]() che notoriamente ammette due soluzioni reali
che notoriamente ammette due soluzioni reali ![]()
Gli studenti sono allenati a trasformare queste equazioni in parabole e a riconoscere le intersezioni con gli assi, le simmetrie, la posizione del vertice in forma analitica. In questo modo costruiscono quella sensibilità matematica essenziale per gli studi scientifici: la geometria algebrica, ovvero matematizzare la geometria.
Potremmo dire – con un gioco di parole – che l’algebra geometrica complementa questo allenamento geometrizzando la matematica.
Per questo esercizio, infatti, vogliamo vedere quell’equazione in forma molto più ingenua. Tradotta in parole molto povere, essa dice: “prendiamo una quantità incognita ![]() , eleviamola al quadrato e sottraiamo un’unità. Se tutto questo risulta zero, allora quella quantità
, eleviamola al quadrato e sottraiamo un’unità. Se tutto questo risulta zero, allora quella quantità ![]() è esattamente ciò che stiamo cercando”. Possiamo figurarci che la faccenda si svolga lungo l’asse reale: avremo allora due quantità che si sommano algebricamente (possiamo usare due vettori) e saremo soddisfatti quando la somma coinciderà con l’origine.
è esattamente ciò che stiamo cercando”. Possiamo figurarci che la faccenda si svolga lungo l’asse reale: avremo allora due quantità che si sommano algebricamente (possiamo usare due vettori) e saremo soddisfatti quando la somma coinciderà con l’origine.
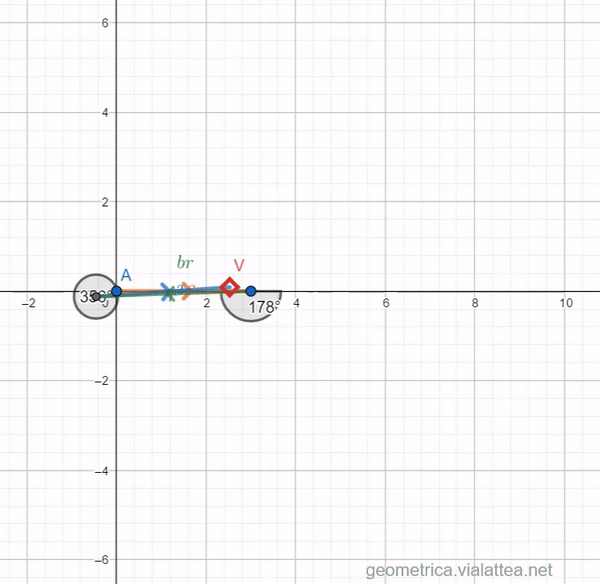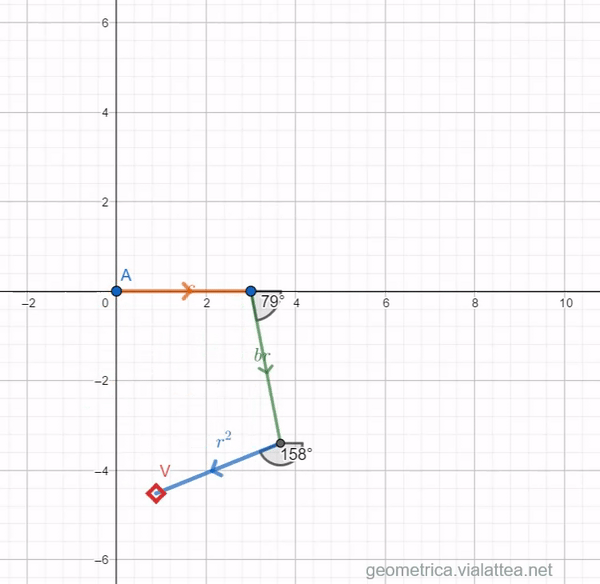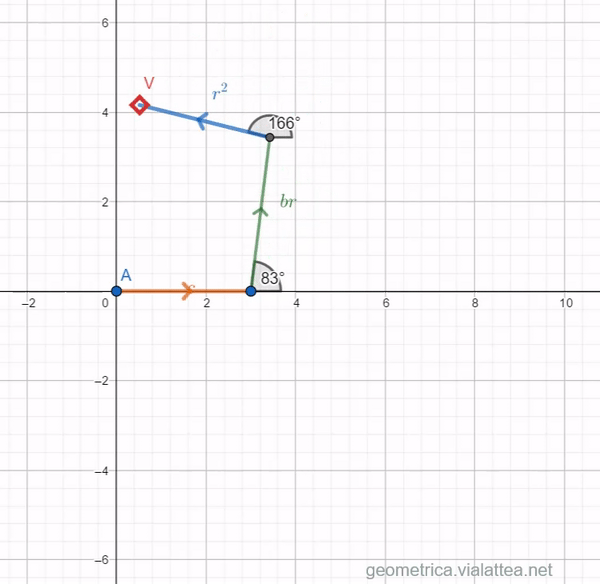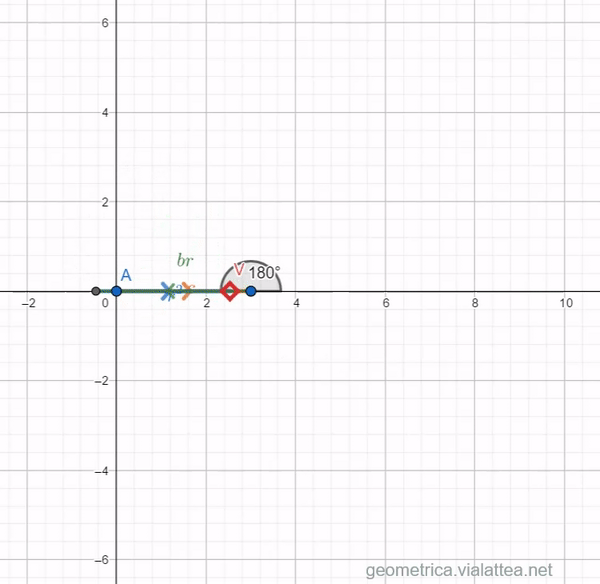
Dopo aver predisposto l’app (check sulla casella Re per indicare le soluzioni reali ed i coefficienti corretti) si può agire sullo slider che prova tutti i valori di ![]() : si potrà verificare che il valore
: si potrà verificare che il valore ![]() della funzione coinciderà con l’origine quando
della funzione coinciderà con l’origine quando ![]() Si può giocare liberamente, ad esempio con l’equazione
Si può giocare liberamente, ad esempio con l’equazione ![]() per trovare geometricamente le soluzioni.
per trovare geometricamente le soluzioni.
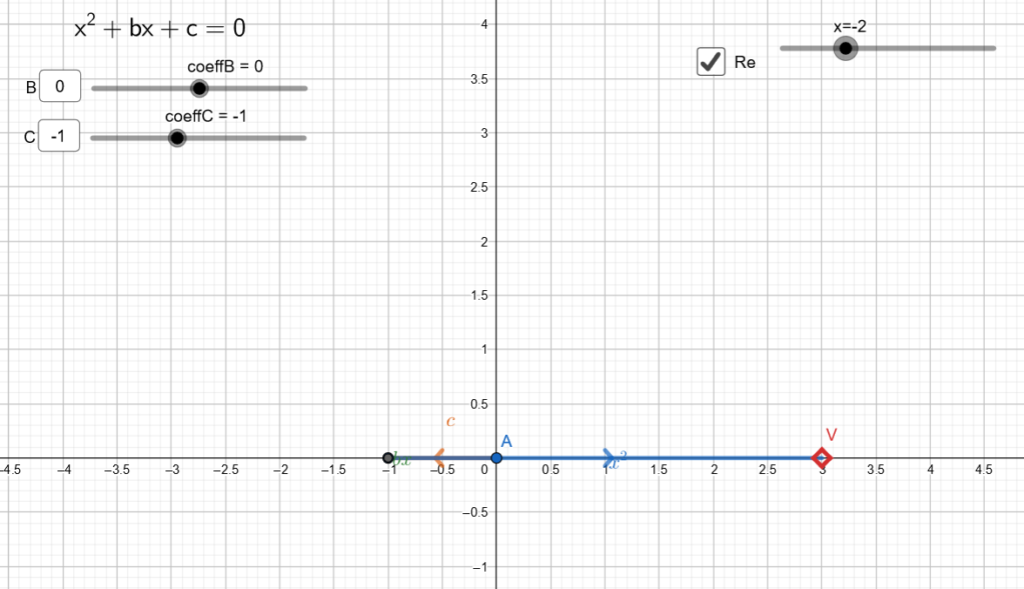
Se ora rappresentiamo l’equazione ![]() ci accorgiamo che il punto V non riesce mai a raggiungere l’origine. Dobbiamo accedere ad un grado di libertà ulteriore: poter cioè ruotare i vettori nel piano, oltre che scalarli: è l’unico modo per poter raggiungere l’origine.
ci accorgiamo che il punto V non riesce mai a raggiungere l’origine. Dobbiamo accedere ad un grado di libertà ulteriore: poter cioè ruotare i vettori nel piano, oltre che scalarli: è l’unico modo per poter raggiungere l’origine.
Se togliamo la spunta dalle soluzioni reali, la situazione si anima con uno slider in più, che corrisponde al secondo parametro della nostra incognita: l’angolo di rotazione. Quindi ora non indicheremo l’incognita con la ![]() che esprime solamente un numero reale dotato di segno, ma indicheremo
che esprime solamente un numero reale dotato di segno, ma indicheremo ![]() o ancora meglio
o ancora meglio ![]()
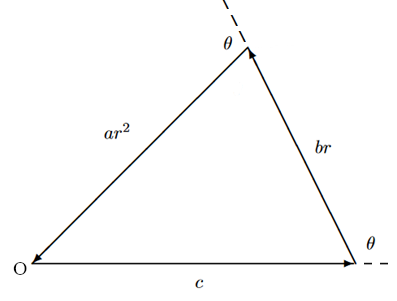
Rimane da capire come rappresentare i termini dell’equazione quando l’incognita è una rotazione: se il termine noto è un semplice vettore reale ed il termine lineare è un vettore scalato di ![]() e ruotato di
e ruotato di ![]() , il termine quadratico sarà scalato di un fattore
, il termine quadratico sarà scalato di un fattore ![]() e ruotato di
e ruotato di ![]() .
.
Questi tre vettori si sommano e se la figura si chiude in un triangolo, ovvero nell’origine, la rotazione ![]() è una soluzione dell’equazione di secondo grado.
è una soluzione dell’equazione di secondo grado.
Proviamo con l’equazione ![]()
Il triangolo si chiude quando ![]() e
e ![]() oppure
oppure ![]() perché le due soluzioni sono simmetriche, se i coefficienti dell’equazioni sono reali (cfr. teorema fondamentale dell’algebra).
perché le due soluzioni sono simmetriche, se i coefficienti dell’equazioni sono reali (cfr. teorema fondamentale dell’algebra).
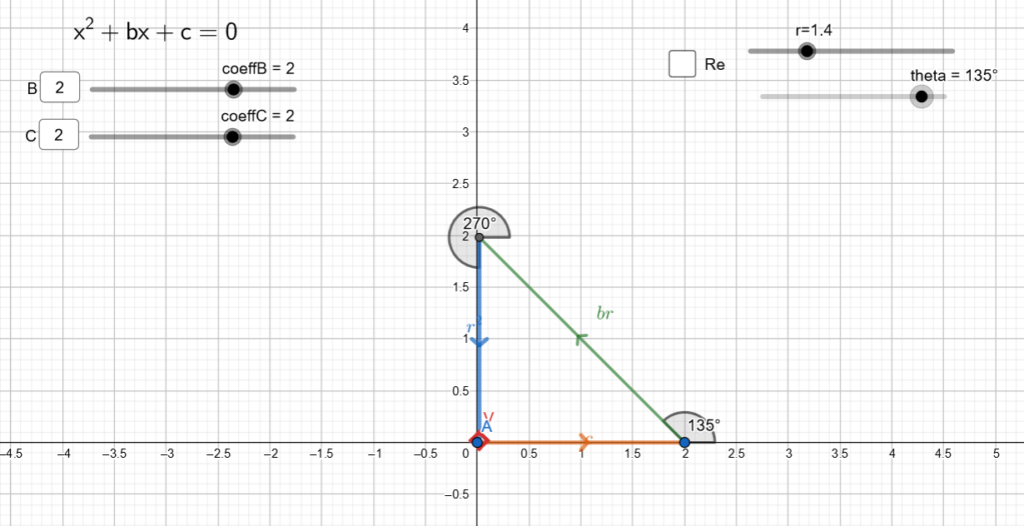
Naturalmente questa è soltanto una dimostrazione visiva: nella scuola secondaria si hanno tutti gli strumenti per poter procedere ad una risoluzione geometrico-analitica. Infatti si vede bene che il triangolo è necessariamente isoscele e quindi si ricava immediatamente ![]() inoltre la perpendicolare al vettore lineare lo divide in due metà e quindi con il teorema di Pitagora si trova anche l’angolo
inoltre la perpendicolare al vettore lineare lo divide in due metà e quindi con il teorema di Pitagora si trova anche l’angolo ![]() .
.
Ad esempio per il caso sopra illustrato, ![]() e si ricava che gli angoli uguali valgono ciascuno
e si ricava che gli angoli uguali valgono ciascuno ![]() e quindi le soluzioni sono
e quindi le soluzioni sono ![]()
Se proprio si vuole il numero complesso, si ricava facilmente che ![]() ma a questo punto sarà evidente che considerare i numeri complessi come rotazioni+dilatazioni riesce ad arricchire di senso geometrico un problema puramente algebrico.
ma a questo punto sarà evidente che considerare i numeri complessi come rotazioni+dilatazioni riesce ad arricchire di senso geometrico un problema puramente algebrico.
