I noti vettori e la sottoalgebra pari, che abbiamo chiamato numeri complessi generalizzati, sono due sottoinsiemi dell’algebra geometrica 2D.
Quali interazioni esistono tra questi due mondi? Lo scopriamo con questi semplici calcoli di prova.
Prendiamo due vettori come rappresentanti del grado dispari di ![]() :
:
![]()
![]()
la loro combinazione lineare di ![]() genera lo spazio vettoriale
genera lo spazio vettoriale ![]() che rappresentiamo con un piano. Abbiamo poi altri due elementi, stavolta membri di
che rappresentiamo con un piano. Abbiamo poi altri due elementi, stavolta membri di ![]() :
:
![]()
![]()
anche loro per combinazione lineare ![]() generano un sottospazio di
generano un sottospazio di ![]() che possiamo rappresentare con un piano.
che possiamo rappresentare con un piano.
Adesso vediamo cosa succede quando moltiplichiamo tra loro questi elementi:
![]()
![]()
![]()
Quindi il prodotto di due vettori – come avevamo già visto – genera un numero complesso. Se i vettori sono unitari questo numero complesso prende il nome di rotore perché è in grado di operare una rotazione su un vettore senza alterarne il modulo, cosa che vediamo subito:
![]()
![]()
![]()
Il risultato, quindi, è ancora un vettore. Non è chiarissimo cosa sia successo, guardando all’algebra dei coefficienti. Molto più chiaro se lo vediamo in azione sul piano tracciando i vettori.
Infine guardiamo cosa succede moltiplicando due numeri complessi:
![]()
che è ancora un numero complesso nel quale possiamo vedere l’uno ruotato dall’altro o viceversa.
Quindi, riassumendo, ecco le interazioni tra vettori e numeri complessi:
| · | ||
ruotato di scalato di | ||
ruotato di scalato di |
Occorre tenere ben presente che è sbagliato identificare i numeri complessi come vettori, nonostante siano entrambi rappresentabili su un piano, per diversi motivi.
- nel piano vettoriale la simmetria viene rotta dalle due direzioni privilegiate
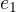 ed
ed 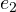 , mentre nel piano dei numeri complessi c’è solo una direzione privilegiata: quella dell’asse
, mentre nel piano dei numeri complessi c’è solo una direzione privilegiata: quella dell’asse 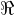 , mentre sussiste una totale libertà rotazionale (il bivettore, per sua natura, non individua una direzione bensì un orientamento rotatorio).
, mentre sussiste una totale libertà rotazionale (il bivettore, per sua natura, non individua una direzione bensì un orientamento rotatorio).
Di conseguenza andrebbe differenziata la rappresentazione:
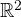
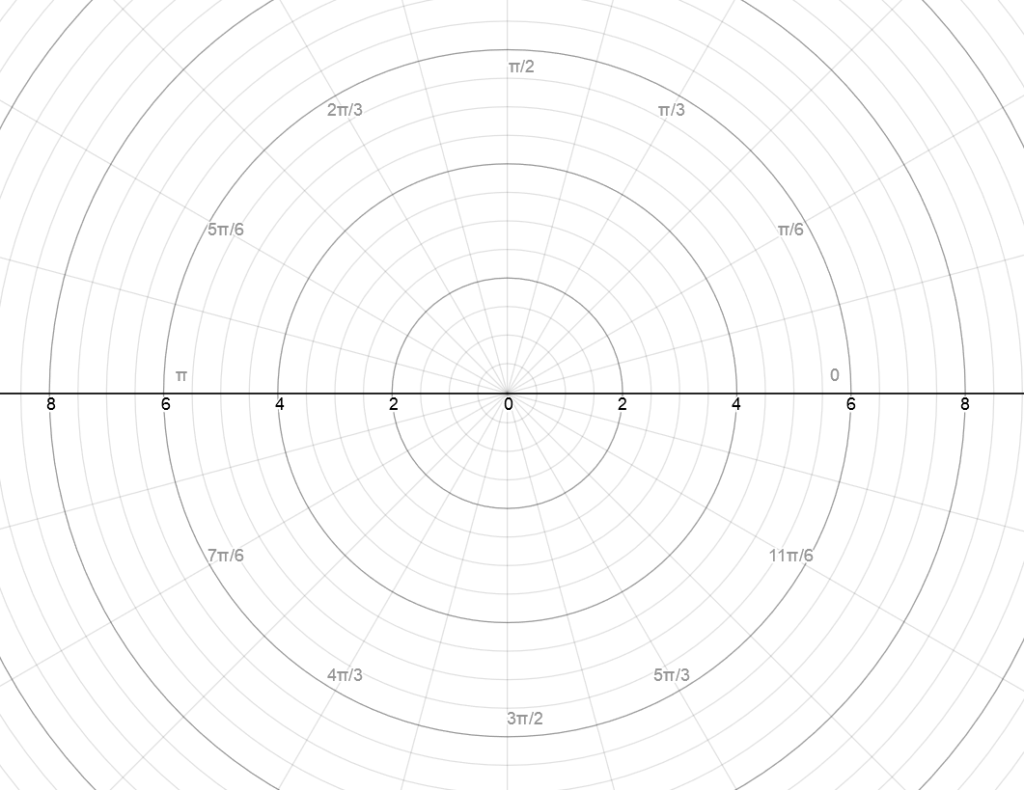
- I vettori rappresentano le traslazioni 2D, i numeri complessi le rotodilatazioni 2D e non vanno confusi, anzi, nella scuola superiore andrebbe insegnata prima possibile questa distinzione, ad esempio fin dalle equazioni di secondo grado.
- l’espressione dell’inverso non coincide: per i vettori l’inverso è dato da
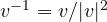 , mentre per i numeri complessi abbiamo
, mentre per i numeri complessi abbiamo 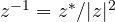 . La coniugazione è ciò che differenzia le due espressioni e graficamente la differenza è ben visibile:
. La coniugazione è ciò che differenzia le due espressioni e graficamente la differenza è ben visibile:
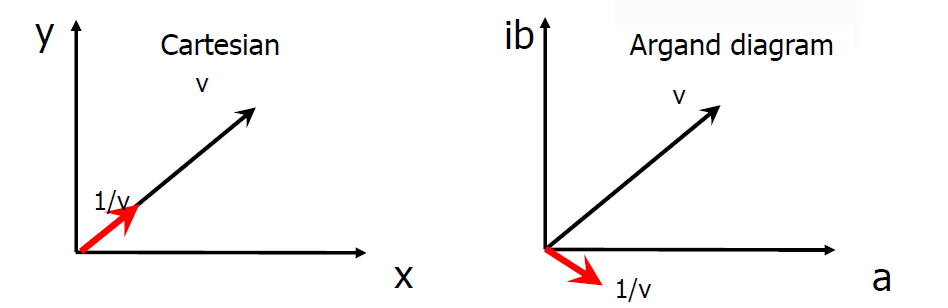
Questo fatto nasconde una insidia molto pericolosa: se ragioniamo su una quantità ![]() rappresentata sull’asse reale, dato che il coniugato coincide col vettore stesso, potremmo non accorgerci mai che l’espressione corretta da usare nei calcoli debba prevedere il coniugato
rappresentata sull’asse reale, dato che il coniugato coincide col vettore stesso, potremmo non accorgerci mai che l’espressione corretta da usare nei calcoli debba prevedere il coniugato ![]() , come nel caso della potenza elettrica in regime alternato.
, come nel caso della potenza elettrica in regime alternato.
Assodato che i vettori ed i complessi NON sono la stessa cosa, nonostante operino entrambi in due dimensioni, resta da chiederci – dato che fanno parte della stessa algebra – in che modo possano “comunicare” questi due mondi. In altre parole, come possiamo mappare vettori su numeri complessi e viceversa.
Come già detto, un numero complesso è un operatore di rotodilatazione. Possiamo allora vederlo come un operatore che prende in ingresso il vettore reale unitario e lo trasforma ruotandolo e scalandolo in base al numero complesso. Il risultato sarà un vettore associato a quel numero complesso: ![]() e quindi possiamo interpretare i numeri complessi come il quoziente tra un vettore ed il vettore unitario:
e quindi possiamo interpretare i numeri complessi come il quoziente tra un vettore ed il vettore unitario: ![]() ovvero quell’espressione che prende la “materia prima”
ovvero quell’espressione che prende la “materia prima” ![]() e la mappa in tutto il piano.
e la mappa in tutto il piano.
Quindi se vogliamo vettorializzare correttamente un numero complesso, lo dobbiamo moltiplicare per il vettore che noi riteniamo esprimere la parte reale (diciamo ![]() ):
): ![]() e scopriremo che possiamo costruire frattali rimanendo in uno spazio vettoriale!
e scopriremo che possiamo costruire frattali rimanendo in uno spazio vettoriale!
Chiudiamo con questa tabella che riassume analogie e differenze tra due, anzi tre mondi che si assomigliano tanto da poter essere confusi:
| Vettori | Numeri complessi | Numeri complessi generalizzati (AG) |
|---|---|---|
| segmenti orientati nel piano | punti in un piano x-iy (piano di Argand-Gauss) | archi orientati di cerchio nel piano |
| assi privilegiati | assi privilegiati | totale simmetria rotazionale |
