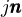La fisica del Novecento, soprattutto dopo la teoria della relatività generale, si è evoluta verso una “geometrizzazione della fisica”. Alcuni hanno persino coniato l’espressione geometrodinamica per sottolineare il fatto che l’equazione centrale della relatività generale esprime il legame tra il tensore energia-impulso e come viene modificata di conseguenza la geometria dello spaziotempo circostante.
Più astratto, invece, è stato il decorso della fisica quantistica, la quale invece si è cristallizzata in spazi matematici più che fisici (es. lo spazio di Hilbert), con abbondante uso di operatori e di grandezze immaginarie che non hanno avuto tentativi di interpretazione geometrica.
Si è affermata così l’idea che la non-commutatività fosse una peculiarità della fisica quantistica e l’idea che le matrici fossero lo strumento necessario per padroneggiarla.
L’algebra geometrica, invece, porta la geometria e la non-commutatività direttamente nel DNA delle espressioni algebriche.
Ecco i principali vantaggi di questo approccio:
- supera la limitazione del prodotto scalare oltre lo spazio 3D
- chiarisce l’ambiguità tra vettori e pseudovettori
- esprime l’unità immaginaria
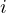 sia come oggetto geometrico che come operatore di rotazione o di dualità, riuscendo ad estendere l’analisi complessa oltre il 2D
sia come oggetto geometrico che come operatore di rotazione o di dualità, riuscendo ad estendere l’analisi complessa oltre il 2D - esprime le rotazioni e le trasformazioni di Lorentz con semplici moltiplicazioni algebriche
- unifica il linguaggio della meccanica classica con quello della meccanica quantistica (uso di spinori ed operatori di proiezione spiegati in senso geometrico)
- riconduce le matrici di Pauli e di Dirac alle basi dell’algebra geometrica rispettivamente
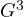 e
e 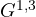
Una nota preliminare riguarda le unità di misura: l’analisi dimensionale in fisica è molto importante e permette di controllare la correttezza di un calcolo o addirittura di ricavare certe espressioni partendo da considerazioni dimensionali.
Con una battuta, la fisica è un linguaggio fortemente tipizzato.
Detto questo, però, l’uso di più grandezze accorpate nello stesso multivettore non è proibito, purché si tenga ben presente che l’unità di misura fa parte del coefficiente (il quanto) e non della base (il cosa).
Ad esempio un bivettore ![]() può risultare espresso in metri quadri, ma non significa che l’unità bivettore esprima un’area (il quanto), esprime invece un piano (quale giacitura? quale orientazione?) e dunque va inteso come
può risultare espresso in metri quadri, ma non significa che l’unità bivettore esprima un’area (il quanto), esprime invece un piano (quale giacitura? quale orientazione?) e dunque va inteso come ![]() .
.
A proposito di bivettori, abbiamo già detto che l’AG sostituisce ai prodotti vettoriali i bivettori, ma occorre fare attenzione alle unità di misura: ad esempio il vettore assiale velocità angolare ![]() definito con la regola della mano destra andrà meglio espresso come prodotto esterno (wedge) tra il raggio e la velocità:
definito con la regola della mano destra andrà meglio espresso come prodotto esterno (wedge) tra il raggio e la velocità: ![]() ma così facendo l’unità di misura sarebbe
ma così facendo l’unità di misura sarebbe ![]() , allora lo dobbiamo ridefinire come:
, allora lo dobbiamo ridefinire come:
![]()
In linea molto generale, per approcciare i problemi di fisica utilizzando l’algebra geometrica, si deve:
- utilizzare l’oggetto geometrico adeguato per la grandezza fisica in esame (vedi tabella)
- sostituire il prodotto vettore con il wedge, eventualmente ragguagliando l’unità di misura
- per comodità di calcolo, sostituire ai bivettori la loro espressione duale, ovvero