Frattali niente affatto complessi

Negli anni ’90 i computer venivano messi alla frusta da un programma che faceva trascorrere ore ed ore di delizia ai suoi utenti. Incredibilmente, non stiamo parlando di un videogioco, ma di Fractint. Era un programma gratuito che riusciva a calcolare i frattali in modo incredibilmente veloce e poi con i tasti +, – e <spazio> partiva uno spettacolo psichedelico in cui le straordinarie forme venivano animate da colori mozzafiato, realizzando un trip degno di viaggi … di altro tipo.

La meraviglia dei frattali: un ingrandimento dell’insieme di Mandelbrot

Il fatto, poi, che i frattali nascessero da formule nel campo dei numeri complessi … beh a quel punto mancava solo l’istituzione di un ordine monastico dei matematici frattisti e avremmo chiuso il cerchio.

Le straordinarie forme dell’insieme di Mandelbrot o di Julia infatti sono generati da una formula iterativa semplicissima: $z_{n+1} = z_n^2 + c$
La domanda fondamentale è: come possono forme così ricche derivare da una formula semplicissima? Il segreto sta, naturalmente, nell’iterazione che spiega anche la ripetizione di motivi all’interno delle strutture del frattale, come se fossero variazioni musicali di un tema o elaborazioni di decorazioni di un tempio. In pratica, realizzando una sequenza di trasformazioni affini contrattive (IFS), si possono produrre frattali di qualsiasi forma.

Concentriamoci sull’insieme di Julia: per ogni punto $z$ del piano complesso, calcoliamo $z^2$ e poi aggiungiamo una costante fissa $c$ per tutti i punti. Il numero che otterremo sarà il punto di partenza per un’altra iterazione. Il comportamento di questa successione è molto variabile: può esplodere verso numeri molto grandi, oppure rimanere contenuto, diciamo entro un raggio $r$ dall’origine. Se dopo un certo numero fissato di iterazioni la successione non diverge, affermiamo che il punto appartiene al frattale.
Come ulteriore finezza, possiamo assegnare una sfumatura di colore in base al valore della successione al termine dei calcoli.
Uno dei possibili risultati (che dipendono dalla scelta di $c$ ) è il seguente, ottenuto con $c=(0.32176 + 0.53227 i)$ ed un limite di 50 iterazioni:

Dopo aver presentato i frattali “metodo classico”, vogliamo raggiungere un obiettivo a metà strada tra l’assurdo e l’inutile, ma con la prospettiva di poter finalmente comprendere le caratteristiche dei frattali. Vogliamo eliminare i numeri complessi dai frattali, trasformandoli in operazioni vettoriali e quindi potenzialmente applicabili nella realtà, ad esempio su un foglio di carta.

Come già detto, se vogliamo vettorializzare correttamente un numero complesso, lo dobbiamo moltiplicare per la base che per noi individua la direzione dell’asse reale (diciamo $e_1$ ): $Z = \pmb{v} / e_1$
Quindi la formula del frattale di Julia in forma vettoriale diventerà:

$\pmb{v}_{k+1} e^{-1}_1 = \pmb{v}_k e^{-1}_1\: \pmb{v}_k e^{-1}_1 + c e^{-1}_1$

che è equivalente (moltiplicando a destra per $e^{-1}_1$ ) e considerando che $e^{-1}_1 = e_1$ all’equazione:

$\pmb{v}_{k+1} = \pmb{v}_k e_1\: \pmb{v}_k + c$

che esprime un fatto geometrico: il vettore successivo è pari alla riflessione della base $e_1$ rispetto al vettore precedente a cui si somma il vettore costante $c$ .

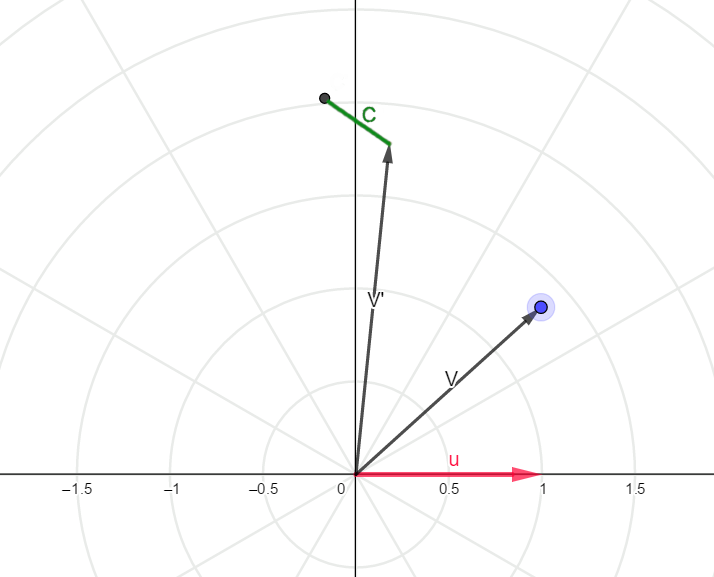
Allora possiamo generare il frattale di Julia in questo modo: per ogni punto del piano rappresentato dal vettore $\vec{v} = (x, y)$ specchiamo la base $e_1$ su questo vettore, lo scaliamo di un fattore $|v|$ e poi sommiamo $c$ . Il vettore risultante sarà sottoposto alle stesse operazioni fino a raggiungere il limite di iterazioni fissato.
Se il risultato è limitato (diciamo interno al cerchio di raggio 2), allora il punto iniziale appartiene all’insieme di Julia.

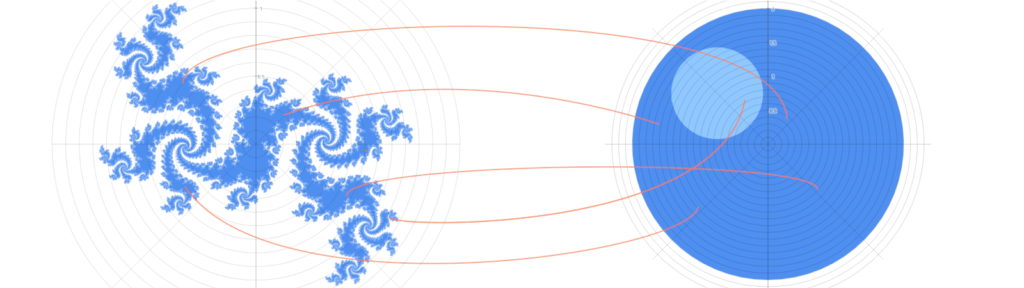
Guardiamo il risultato complessivo: alcuni punti di una forma che all’inizio del processo non conosciamo (infatti, solamente alla fine delle iterazioni sappiamo se il punto appartiene o no all’insieme) si mappano nel cerchio di raggio 2. Allora facciamoci furbi: per generare l’insieme di Julia partiamo dal cerchio di raggio 2 e invertiamo il processo!

I punti del frattale sono quelli che non divergono, quindi si mappano in un cerchio di raggio fissato

$\pmb{v}^{-1}_k\:(\pmb{v}_{k+1} -c)\: \pmb{v}^{-1}_k= e_1$

$\begin{equation} \frac{\pmb{v}}{|v_k|^2}(\pmb{v}_{k+1} -c) \frac{\pmb{v}}{|v_k|^2}= e_1$

Il nuovo processo sarà quindi: partiamo dal cerchio di raggio 2, lo trasliamo in direzione opposta rispetto a $c$ e a questo punto applichiamo la trasformazione inversa: il nuovo vettore sarà sulla bisettrice tra il vecchio vettore ed $e_1$ ed il modulo sarà la radice quadrata.

Partiamo dalla nostra controimmagine, quindi il cerchio di raggio 2

L’operazione inversa consiste nel dispiegamento (qui mostrato quello che si mappa nel semipiano superiore …

… cui segue quello analogo per il semipiano inferiore e il tutto viene ridotto della radice quadrata

Dopo tre iterazioni si comincia ad intuire una forma

Dopo 12 iterazioni si intuisce l’auto-somiglianza

Dopo 128 iterazioni è un frattale vero e proprio.
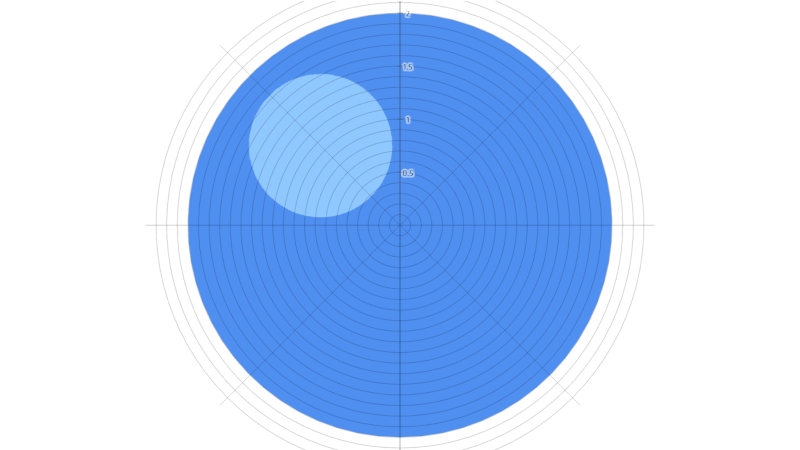
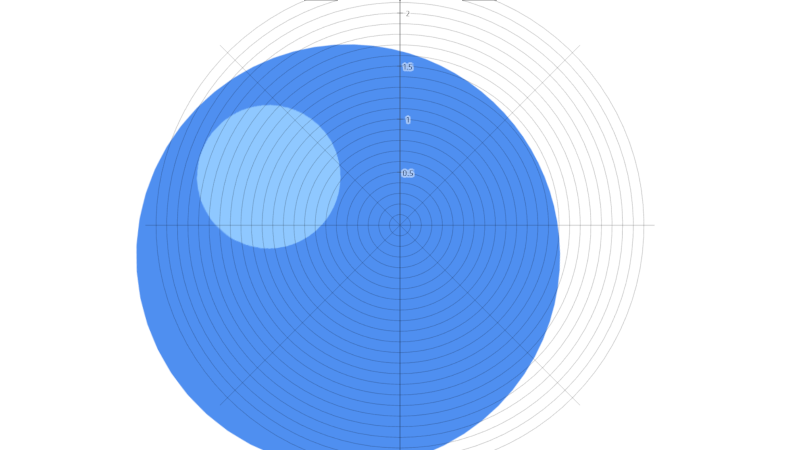
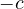
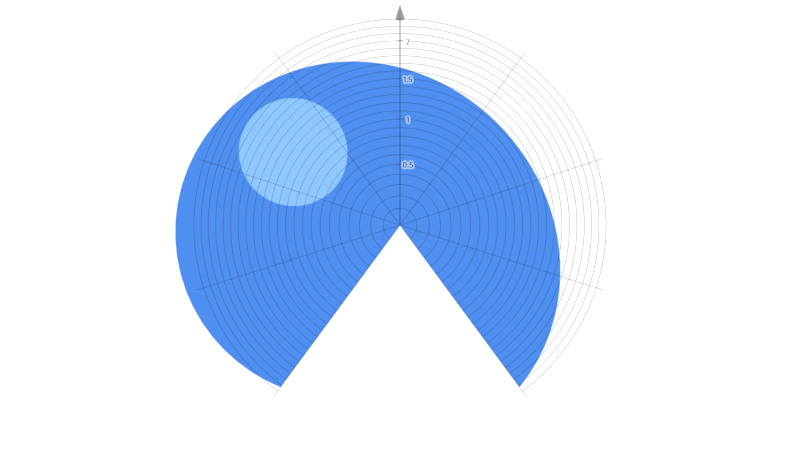
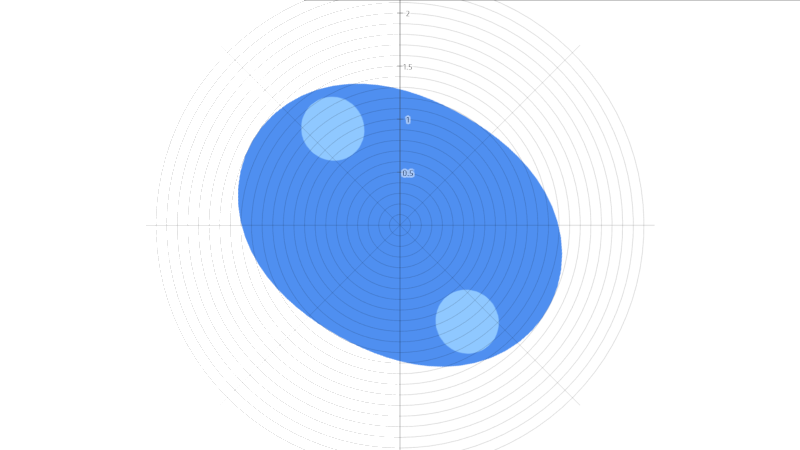
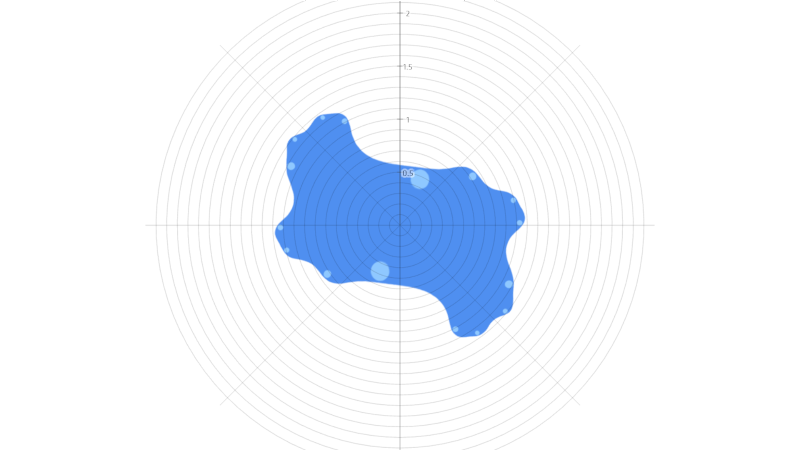
Sequenza tratta dall’eccellente post di Steven Wittens “How to fold a Julia fractal“.

Il fatto straordinario non è solo che abbiamo prodotto un frattale senza ricorrere ai numeri complessi, ma anche il fatto che – come già detto – l’AG scala di dimensione senza difficoltà ed infatti possiamo applicare la medesima formula in 3D ed otteniamo un frattale di Julia 3D, senza ulteriori fatiche.
Che sia bello, poi, è un altro paio di maniche…