La dualità

Il concetto di dualità in fisica è estremamente interessante perché collega aspetti che si possono ritenere opposti, per mezzo di una corrispondenza che invece li porta ad identificarsi nell’aspetto formale, ovvero nelle equazioni.
In questo senso la dualità è la migliore traduzione del suggestivo concetto di coincidentia oppositorum della tradizione filosofica medievale.

Nella fisica la dualità si ritrova largamente nei fenomeni elettrici:

• tensione – corrente
• circuiti serie – circuiti parallelo
• resistenza 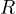– conduttanza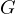
• partitore di tensione – partitore di corrente
• impedenza 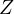– ammettenza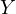
• capacità 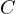– induttanza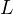
• reattanza 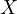– suscettanza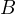
• corto circuito – circuito aperto
• legge di Kirchhoff ai nodi – legge di Kirchhoff alle maglie
• teorema di Thévenin – teorema di Norton

Il principio di dualità, lungi dall’essere confinato ai circuiti, è una delle idee unificanti della fisica moderna. I filosofi della fisica De Haro e Butterfield hanno descritto la dualità come “una simmetria gigante”: una corrispondenza così profonda da identificare due descrizioni apparentemente diverse dello stesso fenomeno. Alcuni esempi celebri:

• elettrico ↔ magnetico: la simmetria delle equazioni di Maxwell nel vuoto;
• posizione ↔ momento: in meccanica quantistica, legate dalla trasformata di Fourier;
• onda ↔ particella: la dualità che sta al cuore della fisica quantistica;
• ordine ↔ disordine (Kramers-Wannier): che lega le alte e le basse temperature in meccanica statistica;

In tutti questi casi ritroviamo la stessa struttura: due facce opposte che le equazioni rivelano essere la medesima cosa — la coincidentia oppositorum di cui parlavamo all’inizio.

Oltre che un interesse speculativo, il principio di dualità ha un risvolto pratico molto amato dagli studenti perché permette di memorizzare solo metà delle formule, perché quelle duali sono immediatamente ricavabili. Ad esempio il condensatore è caratterizzato da questa relazione costitutiva:

sapendo che l’induttanza è la grandezza duale della capacità e che anche tensione e corrente sono grandezze duali, la relazione duale si ricava immediatamente:

Infine il principio di dualità è un principio euristico, cioè serve per scoprire qualcosa di nuovo.
Nel 1825 il matematico francese Joseph Gergonne notò che per ogni teorema in geometria proiettiva che coinvolgeva linee e punti, ne corrispondeva uno duale, cioè ottenuto scambiando i ruoli di linee e punti. Ad esempio al teorema in 2D “due punti definiscono una linea” corrisponde “due linee si incontrano in un punto” oppure al teorema in 3D “tre punti definiscono un piano” corrisponde “tre piani si intersecano in un punto”.

Nell’algebra la nozione di dualità corrisponde al complemento ortogonale, ovvero al sottospazio formato da tutte le basi che non formano l’elemento.

La relazione di dualità è talmente importante nell’AG da avere un simbolo dedicato, l’asterisco $^*$ (star). Il duale di un multivettore si ottiene moltiplicando per lo pseudoscalare unitario. Qui sorge però una questione di convenzione: noi adottiamo, coerentemente con la pagina convenzioni, la moltiplicazione a destra per l’inverso dello pseudoscalare,$$M^* = M\,I^{-1}$$definizione usata da Hestenes e da A. MacDonald (vedi riferimenti). Altri autori, ad esempio Doran in [7], definiscono il duale come $M^* = MI$. Attenzione: le due definizioni non sono equivalenti, perché in 3D vale $I^{-1} = -I$ e quindi $MI^{-1} = -MI$: i due duali differiscono per il segno. È proprio questa libertà di convenzione (a destra o a sinistra, con $I$ o con $I^{-1}$) la ragione per cui nel duale “compare sempre un segno che sembra ballare”. Una volta fissata la convenzione $M^* = MI^{-1}$, però, il segno è determinato una volta per tutte.

Ad esempio il duale del piano individuato dalle basi

Se invece partiamo dal vettore dovremo utilizzare la trasformazione inversa e quindi

quindi occorre prestare attenzione alla direzione in cui stiamo effettuando l’operazione di dualità: da vettori a bivettori oppure il contrario.

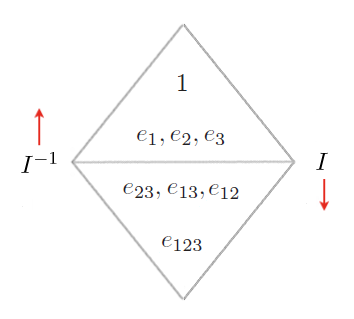
E’ interessante notare che laddove , quindi in 2D e in 3D, il duale del duale di un elemento non coincide con l’elemento stesso: vi è un segno meno a fare la differenza. Ad esempio


quindi servono due cicli di dualità per riportarci all’elemento originario.
In generale in uno spazio di dimensione avremo .

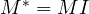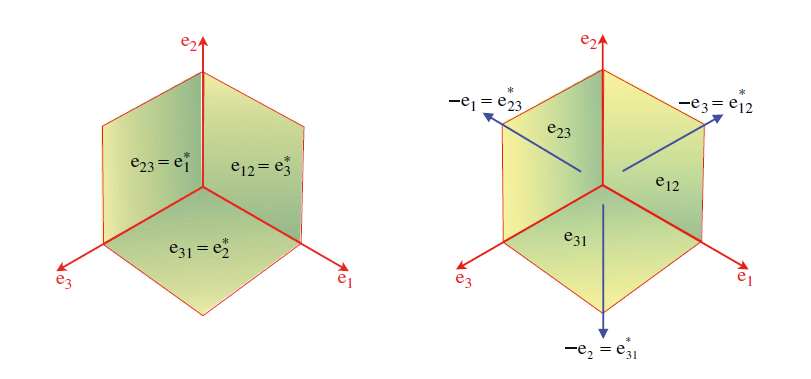
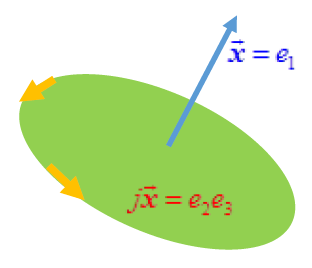
La relazione di dualità è stata usata inconsapevolmente per decenni nell’algebra vettoriale: infatti i fantomatici vettori assiali non sono altro che bivettori mascherati, come si vede in figura

Come esercizio, calcoliamo il duale del prodotto esterno :

poiché in 3D lo pseudoscalare I commuta con ogni elemento. Dunque, svolgendo:

Riconosciamo nell’espressione finale il classico prodotto vettoriale!
Dunque tra prodotto esterno e prodotto vettoriale c’è una relazione di dualità.
Vale anche la relazione inversa:

È importante sottolineare una differenza tra il duale di un multivettore e il suo complemento ortogonale. La differenza è sottile ma importante. Il complemento ortogonale di un piano è la retta a esso perpendicolare: un sottospazio, cioè un insieme di direzioni, privo di lunghezza e di verso. Il duale di quel piano, invece, è un vettore ben preciso, con un modulo (proporzionale all’area del piano) e un’orientazione (coerente con quella del piano). In altre parole: il complemento ortogonale ti dice dove sta l’oggetto duale, ma è la dualità a dirti quanto è grande e in che verso punta.

C’è una conseguenza notevole in tutto questo. La famigerata “regola della mano destra” — quella che tormenta ogni studente di fisica — non è una legge di natura: è semplicemente la scelta dell’orientazione dello pseudoscalare. Tutta l’arbitrarietà della “manualità” si concentra in un unico punto, il segno di $I$ (scegliere $I = e_1e_2e_3$ anziché $e_3e_2e_1$​ equivale a dichiarare destrorsa la terna delle basi).

Lo si vede bene scomponendo il prodotto vettoriale $\pmb{a}\times\pmb{b} = (\pmb{a}\wedge\pmb{b})\,I^{-1}$: il bivettore $\pmb{a}\wedge\pmb{b}$ è un oggetto del tutto intrinseco, un’area orientata nel suo piano, che non “sa” nulla di destra o sinistra. La chiralità entra in scena soltanto nel momento in cui moltiplichiamo per $I$ per ottenere il vettore assiale: è lì, e solo lì, che dobbiamo decidere “da quale lato del piano” punta l’asse. Capovolgi l’orientazione di $I$ e il prodotto vettoriale cambia verso — ma il bivettore resta identico.

In altre parole, la mano destra è una proprietà del duale (l’artificio che traveste un bivettore da vettore), non della geometria sottostante. Lavorando direttamente con i bivettori, come abbiamo visto parlando dei vettori assiali, il problema semplicemente svanisce: non serve nessuna mano.