i non è più immaginario – Algebra geometrica

Quando abbiamo costruito l’algebra geometrica dello spazio abbiamo dimostrato che il quadrato di un bivettore unitario $e_1e_2$ , ovvero l’unità di area orientata vale -1 e così pure il quadrato del volume unitario, ovvero il trivettore $e_1e_2e_3$

E’ davvero un risultato spiazzante: vai a spiegare in parole semplici com’è possibile che il quadrato di una entità geometrica tangibile valga un numero negativo! Per ora dobbiamo fermarci qui, ricordiamo solamente che è importantissimo il concetto di orientazione. Infatti nell’algebra geometrica non basta definire l’area come entità geometrica: è fondamentale il segno.

A questo punto la tentazione è fortissima:
il bivettore unitario $e_1e_2$ si identifica con l’unità immaginaria $i$ dei numeri complessi?
quindi anche il trivettore unitario $e_1e_2e_3$ ?
se il quadrato di entrambi vale -1, rappresentano la stessa unità immaginaria?
Sono domande legittime, ma qui è necessaria un po’ di cautela.

Prima le notizia buone.
Riusciamo a fatica a contenere la soddisfazione di vedere finalmente che l’unità immaginaria $i$ ha un corpo ed un comportamento.
Diciamo corpo per indicare che non si tratta più di una entità talmente astratta da risultare inesistente: ce l’abbiamo davanti agli occhi e lo è stata per secoli davanti agli occhi dei matematici.
L’unità immaginaria va identificata con la porzione unitaria del bivettore. E’ un pezzetto orientato di piano. Diciamo comportamento perché è ancora più interessante vedere l’effetto che fa sugli altri enti geometrici. Proviamo a giocarci un po’ usando come cavia un vettore generico, che moltiplicheremo per $i = e_1e_2$ prima a destra e poi a sinistra:

$\pmb{a} = a_1 e_1 + a_2 e_2$
$\pmb{a}\: (e_1e_2) = a_1e_2 - a_2 e_1$
$(e_1e_2)\:\pmb{a} = - a_1e_2 + a_2 e_1$

Quindi la moltiplicazione a destra per $e_1e_2$ (che ha orientazione antioraria) provoca una rotazione di $\pi/2$ in senso antiorario, mentre la moltiplicazione a sinistra inverte il senso della rotazione. Da questo punto di vista il bivettore $e_1e_2$ si differenzia da $i$ perché non commuta, anzi anticommuta con i vettori.
Attenzione: noi siamo abituati a vedere l’operatore che “attacca” il suo operando da sinistra, ma in questo caso è l’operazione da destra che conserva l’orientazione!

Come abbiamo accennato prima, sottolineiamo una dualità interessantissima: ogni elemento dell’AG può essere visto come oggetto ma anche come operatore. A scuola i numeri complessi vengono visti quasi esclusivamente come oggetti, staticamente fissati nel piano di Argand-Gauss come punti cartesiani. Nell’AG, invece, acquistano una dimensione attiva, diventando operatori di rotodilatazione.
Una seconda accezione li vede come operatori di dualità, che trasformano elementi dell’algebra $\mathbb{G}^n$ di grado $r$ in elementi speculari di grado $n-r$ .

La cattiva notizia è che non possiamo identificare quattro concetti distinti, anche se algebricamente si comportano in modo simile:

il bivettore unitario 2D $e_1 e_2$
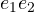
i tre bivettori 3D $e_1 e_2$ , $e_2 e_3$ , $e_3 e_1$
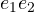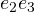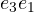
il trivettore unitario 3D $e_1 e_2 e_3$
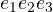
l’unità immaginaria 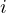$i$ dei numeri complessi

Tutti questi elementi quadrano a -1, ma non basta per dire che sono la stessa cosa. Occorre infatti considerare la commutatività, che vale per $i$ e per il trivettore $e_1e_2e_3$ , ma non vale per i bivettori.

Dovremo quindi utilizzare simboli distinti e quindi manterremo la $i$ per l’unità immaginaria, mentre useremo $I$ per il trivettore 3D, visto che le proprietà coincidono. A volte si usa $I$ anche per il bivettore in 2D, ma se il contesto non fosse chiaro, potrebbero essere impiegati i simboli $I_{12}$ o $I_{123}$ .
Molto usata per ragioni storiche anche la $j$ dal mondo elettrotecnico (usando la $i$ si fa confusione con la corrente!).