Nel 1907 il matematico tedesco Herrmann Minkowski si convinse che la neonata teoria della relatività del suo ex allievo Einstein, basata su precedenti lavori di Poincaré e di Lorentz, potesse essere rappresentata in uno spaziotempo quadridimensionale ma non euclideo, perché il tempo doveva distinguersi dalle dimensioni spaziali.
L’anno seguente formulò compiutamente la sua teoria e la sintetizzò nella famosa frase “d’ora in avanti lo spazio singolarmente inteso, ed il tempo singolarmente inteso, sono destinati a svanire in nient’altro che ombre e solo una connessione dei due potrà preservare una realtà indipendente“.
Questa nuova rappresentazione si rivelò estremamente utile ed aiutò parecchio Einstein nel passo successivo, cioè estendere la relatività alla gravitazione.
Nell’algebra geometrica dunque sfrutteremo per la prima volta quella postilla nascosta in uno degli assiomi: il prodotto di due basi dev’essere un numero reale. Non abbiamo detto positivo, infatti la base che si identifica col tempo si distinguerà dallo spazio proprio per il segno del quadrato.
Avremo allora quattro basi, che cambiano forma perché in relatività si è ormai affermata questa notazione:
![]() (tempo, 3 coordinate spaziali)
(tempo, 3 coordinate spaziali)
Il primo strumento che ci serve è la norma di un vettore, ovvero quanto vale la quantità ![]() . La sequenza dei quattro segni di ciascuna componente si chiama segnatura e in teoria saremmo liberi di scegliere quella preferita dai fisici relativistici (-, +, +, +) o quella preferita dai fisici delle particelle (+, -, -, -). Nessuna teoria fisica permetterebbe di distinguere le due: producono gli stessi identici risultati.
. La sequenza dei quattro segni di ciascuna componente si chiama segnatura e in teoria saremmo liberi di scegliere quella preferita dai fisici relativistici (-, +, +, +) o quella preferita dai fisici delle particelle (+, -, -, -). Nessuna teoria fisica permetterebbe di distinguere le due: producono gli stessi identici risultati.
Nel caso dell’AG, però, questa libertà non c’è: se vogliamo che l’algebra sia consistente, dobbiamo scegliere la seconda, perché è l’unica che arriva ad includere nel modo corretto la sottoalgebra dello spazio tridimensionale! Quindi:
![]()
Questa segnatura mista apre ad alcune novità: un vettore può avere “lunghezza” nulla (vettore di tipo luce) o addirittura negativa (vettore di tipo spazio). In alcuni testi si afferma che questo è tutto ciò che serve per formulare una teoria fisica in ambito relativistico, ma poi si incontrano difficoltà tecniche quando si devono modellare il campo elettromagnetico ed il momento angolare. Si finisce col dover ricorrere a strumenti matematici più complessi (tensori di rango 2 antisimmetrici).
Ma noi sappiamo bene che l’algebra geometrica ha una freccia in più al suo arco: il prodotto geometrico. E’ proprio questo – lo vedremo – a semplificare straordinariamente il lavoro, evitando di ricorrere ai tensori.
E’ un investimento che si ripaga alla grande!
Nasceranno allora gli altri componenti dell’algebra dello spaziotempo (abbreviata in STA).
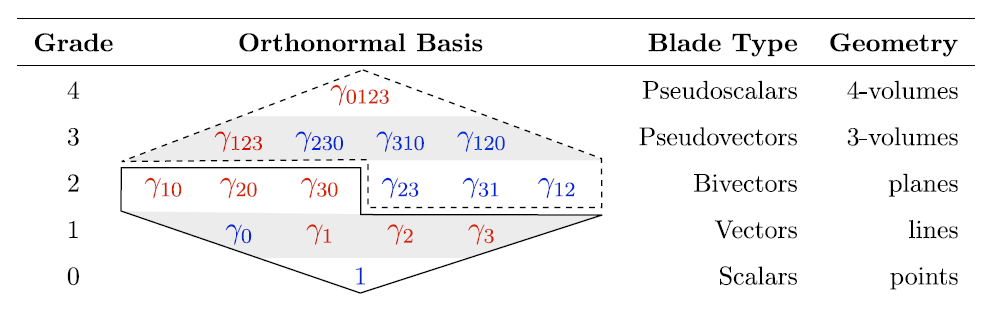
Il colore degli elementi indica la segnatura: positiva in blu, negativa in rosso.
Le aree racchiuse dalle linee continua e tratteggiata si specchiano nella relazione di dualità (moltiplicazione a destra per lo pseudoscalare ![]() ) mentre all’interno dello stesso box, le aree a fondo chiaro e grigio si specchiano nella dualità temporale (moltiplicazione a destra per la base
) mentre all’interno dello stesso box, le aree a fondo chiaro e grigio si specchiano nella dualità temporale (moltiplicazione a destra per la base ![]() ).
).
Da notare che i bivettori temporali sono indicati come ![]() : il motivo sarà chiaro nel seguito.
: il motivo sarà chiaro nel seguito.
E’ notevole il fatto che anche nella STA lo pseudoscalare ![]() e dunque lo possiamo indicare ancora una volta col simbolo
e dunque lo possiamo indicare ancora una volta col simbolo ![]() . Inoltre
. Inoltre ![]() ed anticommuta con vettori e trivettori mentre, come sempre, commuta con tutti gli elementi di grado pari.
ed anticommuta con vettori e trivettori mentre, come sempre, commuta con tutti gli elementi di grado pari.
Il generico multivettore dunque sarà la combinazione di tutti i gradi:
![]()
ma noi sfrutteremo la dualità per ridurlo alla forma complessificata:
![]()
con la particolarità che ![]()
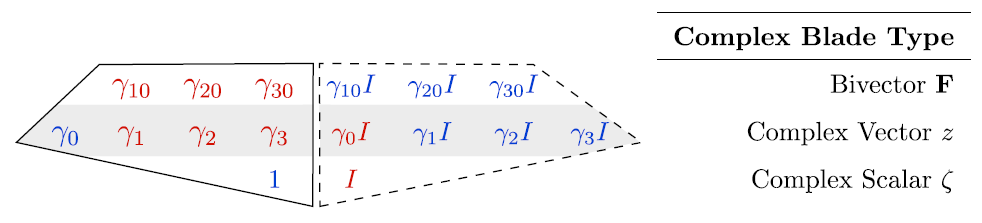
La struttura complessa dimezza i gradi della STA lasciando come enti irriducibili i bivettori, che non possono essere ulteriormente scomposti.
I bivettori nella STA
Dunque i protagonisti indiscussi della STA sono i bivettori.
I tre bivettori base di tipo spazio, come abbiamo già visto, hanno quadrato negativo e vale l’identità fondamentale:
![]()
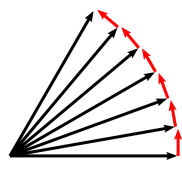
e quindi generano le rotazioni ordinarie.
Invece il fatto che vi sia la base ![]() di tipo tempo tra i componenti dei tre bivettori misti spazio-tempo determina una differenza sostanziale: il quadrato del bivettore stavolta è positivo. I bivettori a norma positiva hanno un certo numero di proprietà nuove, rispetto a quelli che già conoscevamo e la più importante è questa:
di tipo tempo tra i componenti dei tre bivettori misti spazio-tempo determina una differenza sostanziale: il quadrato del bivettore stavolta è positivo. I bivettori a norma positiva hanno un certo numero di proprietà nuove, rispetto a quelli che già conoscevamo e la più importante è questa:
![]()
quindi in questi bivettori abbiamo a che fare con una geometria iperbolica, infatti essi non generano una rotazione e lo vediamo bene con due semplici prove:
![]()
![]()
la pseudo-rotazione generata dai bivettori misti viene chiamata col termine inglese boost che significa variazione di velocità.
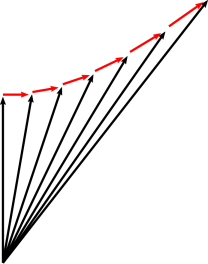
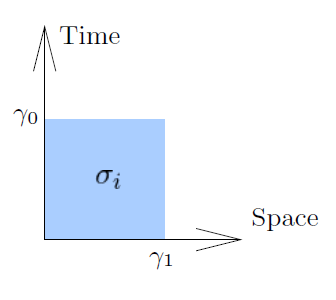
Da notare che per rispettare la tradizione che vede questi diagrammi con il tempo in ordinata e lo spazio in ascissa, il bivettore va indicato come ![]() ovvero destrorso.
ovvero destrorso.
Questi bivettori spaziotemporali hanno una notazione dedicata:![]()
la loro importanza deriva dal fatto che – pur essendo propriamente bivettori – sono da considerarsi vettori nel sistema di riferimento perpendicolare all’asse temporale ![]() e per questo sono chiamati vettori relativi, dove l’aggettivo relativo va inteso come rispetto alla velocità del sistema di riferimento.
e per questo sono chiamati vettori relativi, dove l’aggettivo relativo va inteso come rispetto alla velocità del sistema di riferimento.
Quindi, dato un bivettore spaziotemporale, basterà moltiplicarlo a destra per ![]() per estrarne la componente spaziale
per estrarne la componente spaziale ![]() in quel sistema di riferimento.
in quel sistema di riferimento.
Più in generale, ![]() determina la mappatura di ogni vettore spaziotemporale
determina la mappatura di ogni vettore spaziotemporale ![]() come:
come:
![]()
quindi lo scalare è la componente tempo del vettore a ed il bivettore può essere scomposto nelle basi ![]() e rappresenta un vettore spaziale relativo all’osservatore del riferimento
e rappresenta un vettore spaziale relativo all’osservatore del riferimento ![]() .
.
La lettera ![]() non è presa a caso, perché questi bivettori spaziotemporali si comportano esattamente come le matrici di Pauli, elaborate per spiegare il fenomeno dello spin nella fisica quantistica.
non è presa a caso, perché questi bivettori spaziotemporali si comportano esattamente come le matrici di Pauli, elaborate per spiegare il fenomeno dello spin nella fisica quantistica.
Come si è visto nei casi 2D e 3D, le sottoalgebre pari hanno una importanza che deriva dal fatto che sono isomorfe ad algebre note, rispettivamente a ![]() e ad
e ad ![]() , ovvero ai numeri complessi e ai quaternioni.
, ovvero ai numeri complessi e ai quaternioni.
La sottoalgebra pari della STA è formata da scalari, dai 6 bivettori e dallo pseudoscalare.
E’ interessante notare che questi elementi si possono mappare nella ordinaria algebra dello spazio tridimensionale! Infatti lo pseudoscalare è il medesimo: ![]()
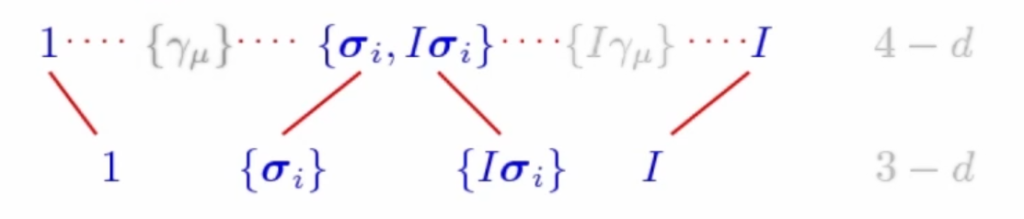
I vettori relativi si mappano sui vettori ordinari 3D ed i bivettori relativi su quelli ordinari 3D.
Questa interessante scomposizione dipende dall’osservatore, perché tutto è legato allo specifico asse temporale ![]() .
.
