Il prodotto scalare tra due vettori è dato dal modulo del primo per il componente del secondo lungo il primo (proiezione), ma siccome è una forma bilineare simmetrica, vale anche l’inverso, cioè la proiezione del primo sul secondo. 
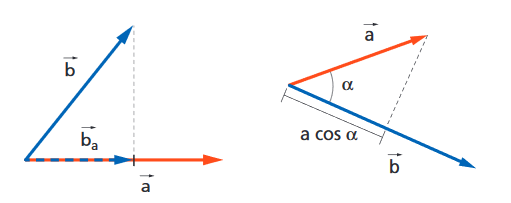
Il prodotto scalare combina due vettori in una grandezza scalare, il che fa immediatamente capire che la ricchezza della loro informazione spaziale viene persa.
Infatti, se rappresentiamo due vettori 
e 
, e la proiezione di su , ci accorgiamo che possiamo individuare infiniti vettori di lunghezza e direzione diversa, che lasciano invariata la proiezione.
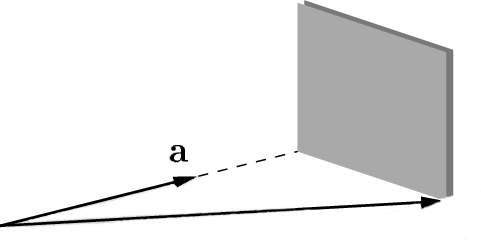
Estendendo il ragionamento in tre dimensioni, ci accorgiamo che il luogo dei vettori con proiezione data su è un piano perpendicolare ad e passante per l’estremo della proiezione di un qualsiasi vettore su .
Dal punto di vista algebrico, il calcolo del prodotto scalare è semplice: si tratta della somma dei prodotti delle componenti omonime: