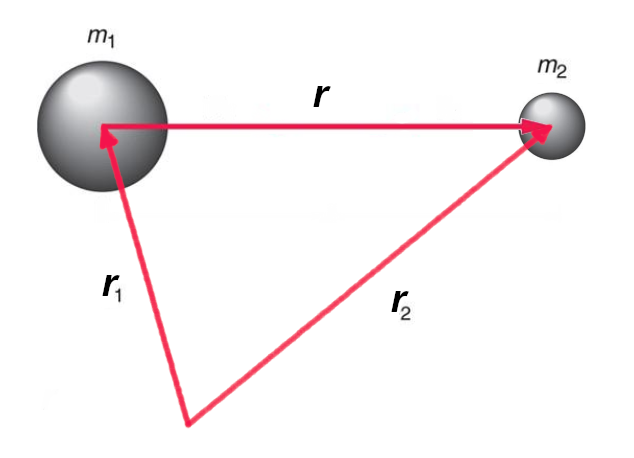
Passiamo ora a trattare il moto dei pianeti, che risponde alla legge di gravitazione universale scoperta dal grande Newton. Schematizziamo la situazione con due corpi di massa ![]() e
e ![]() che si trovano ad una certa distanza
che si trovano ad una certa distanza ![]() ed
ed ![]() rispetto ad un punto preso come riferimento.
rispetto ad un punto preso come riferimento.
La distanza reciproca ![]() vale
vale ![]() . Questi due corpi si attraggono con una forza diretta lungo la congiungente, che varia con l’inverso del quadrato della distanza ed è proporzionale alle loro masse:
. Questi due corpi si attraggono con una forza diretta lungo la congiungente, che varia con l’inverso del quadrato della distanza ed è proporzionale alle loro masse:
![]()
Per semplificare, ![]() sarà molto maggiore di
sarà molto maggiore di ![]() , come accade per i pianeti attorno al Sole o per i satelliti attorno al loro pianeta. Quindi possiamo scrivere per l’accelerazione di
, come accade per i pianeti attorno al Sole o per i satelliti attorno al loro pianeta. Quindi possiamo scrivere per l’accelerazione di ![]() la forma alternativa, più compatta:
la forma alternativa, più compatta:
![]()
Dove ![]() ed il segno è giustificato dal fatto che il raggio vettore va da
ed il segno è giustificato dal fatto che il raggio vettore va da ![]() a
a ![]() .
.
Se partissimo con il corpo ![]() fermo, il moto sarebbe semplicemente una caduta di moto accelerato e si svolgerebbe lungo la congiungente dei due centri. Nulla di interessante, dunque.
fermo, il moto sarebbe semplicemente una caduta di moto accelerato e si svolgerebbe lungo la congiungente dei due centri. Nulla di interessante, dunque.
La cosa si fa interessante quando il corpo possiede una velocità iniziale in direzione diversa da quella di ![]() . Se avviene questo, il corpo è dotato di una grandezza che si chiama momento angolare o anche momento della quantità di moto.
. Se avviene questo, il corpo è dotato di una grandezza che si chiama momento angolare o anche momento della quantità di moto.
Nella trattazione classica questa grandezza scaturisce dal prodotto vettoriale tra il raggio vettore ![]() e la quantità di moto
e la quantità di moto ![]() :
:
![]()
e ne risulta un vettore assiale, che a noi – lo abbiamo già detto – fa storcere parecchio il naso.
Allora preferiamo esprimerlo in modo più consono all’algebra geometrica come il prodotto esterno tra ![]() e
e ![]() e dunque si tratta di un bivettore:
e dunque si tratta di un bivettore:
![]()
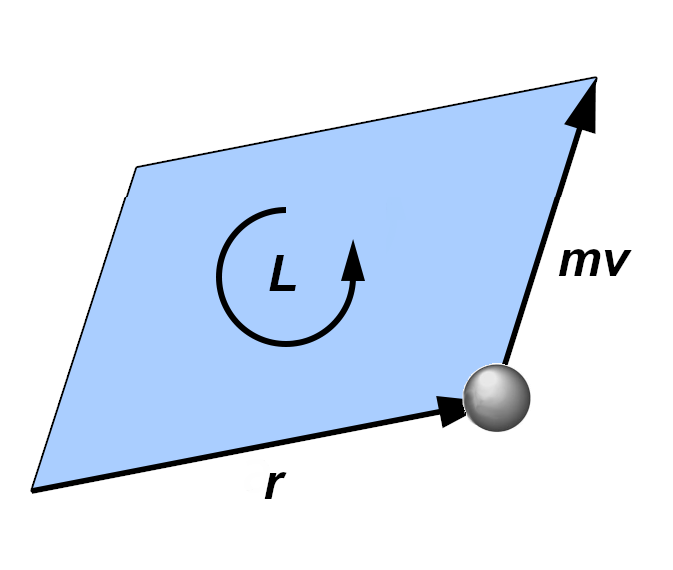
Proprio in quanto bivettore, esso esprime geometricamente l’area spazzata dal raggio vettore durante il moto del corpo ![]() attorno ad
attorno ad ![]() .
.
Un naturalista studia la Natura osservando gli animaletti strani che incontra e li esamina per vedere il comportamento: come si muovono, cosa mangiano, quali suoni emettono, come si riproducono. I fisici lavorano esattamente nello stesso modo. Innanzitutto vediamo come cambia L nel tempo: per conoscerlo calcoliamo la derivata, che in quanto operatore lineare, agisce sul prodotto esterno proprio come nel caso del prodotto di due termini:
![]()
L’ultimo passaggio è giustificato dal fatto che l’accelerazione gravitazionale è rivolta proprio nella direzione ![]() e dunque il prodotto esterno vale zero. In conclusione: nel moto gravitazionale il momento angolare è conservato. Prima conseguenza importante: il moto si svolge in un piano invariabile.
e dunque il prodotto esterno vale zero. In conclusione: nel moto gravitazionale il momento angolare è conservato. Prima conseguenza importante: il moto si svolge in un piano invariabile.
Da questa prima considerazione, se teniamo conto del significato geometrico del prodotto angolare, possiamo già giustificare la seconda legge di Keplero, cioè che l’area spazzata dal raggio vettore è una grandezza costante nel tempo.
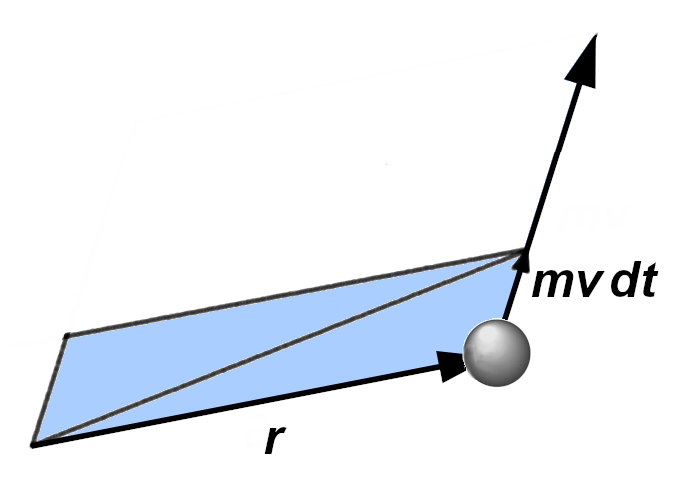
Pensiamo adesso al nostro pianeta che si sposta con velocità ![]() in una direzione generica: vediamo che nel tempo infinitesimo
in una direzione generica: vediamo che nel tempo infinitesimo ![]() il raggio vettore descrive un’area pari a quella del triangolo, ovvero metà del parallelogramma con i lati
il raggio vettore descrive un’area pari a quella del triangolo, ovvero metà del parallelogramma con i lati ![]() ed
ed ![]() ovvero
ovvero
![]()
o anche
![]()
quindi la velocità areale vale metà del momento angolare.
Un’altra costante del moto
Adesso vogliamo sviluppare quel prodotto esterno ![]() che definisce il momento angolare.
che definisce il momento angolare.
Sarà di grandissimo aiuto la tecnica di pensare di scomporre un qualsiasi vettore ![]() come il prodotto tra il modulo
come il prodotto tra il modulo ![]() ed il versore
ed il versore ![]() perché così facendo, quando andiamo a considerare la generica variazione di una grandezza vettoriale, riusciamo a separare il contributo dovuto al cambiamento di lunghezza e al cambiamento di direzione. Per dirla in termini aulici, separiamo i contributi dell’intensità e della geometria.
perché così facendo, quando andiamo a considerare la generica variazione di una grandezza vettoriale, riusciamo a separare il contributo dovuto al cambiamento di lunghezza e al cambiamento di direzione. Per dirla in termini aulici, separiamo i contributi dell’intensità e della geometria.
Dunque: ![]() e dunque:
e dunque:
![]()
ma dato che ![]() è la derivata di
è la derivata di ![]() allora usando la proprietà della derivata di un prodotto:
allora usando la proprietà della derivata di un prodotto:
![]()
ma nello sviluppo dell’espressione il primo termine è nullo perché ![]() e dunque rimane:
e dunque rimane:
![]()
a questo punto richiamiamo la definizione del prodotto geometrico: ![]() , allora:
, allora:
![]()
Immaginiamo ora di osservare il versore ![]() : dobbiamo necessariamento concludere che qualsiasi variazione, non potendo riguardare il modulo, riguarderà la direzione e pertanto il versore della sua variazione nel tempo
: dobbiamo necessariamento concludere che qualsiasi variazione, non potendo riguardare il modulo, riguarderà la direzione e pertanto il versore della sua variazione nel tempo ![]() sarà necessariamente perpendicolare ad
sarà necessariamente perpendicolare ad ![]() e quindi il loro prodotto scalare
e quindi il loro prodotto scalare ![]() è nullo. Dunque:
è nullo. Dunque:
![]()
Questa espressione ci serve per ricavare un’altra costante nel moto dei pianeti. Per trovarla rifacciamoci alla legge di gravità:
![]()
e moltiplichiamo ordinatamente i due membri con l’espressione trovata per il momento angolare, scoprendo con sollievo che molti termini si elidono:
![]()
Possiamo scriverlo nella forma ![]() ovvero
ovvero
![]()
Quindi la quantità ![]() , ed ha natura vettoriale perché dato che
, ed ha natura vettoriale perché dato che ![]() è un bivettore, moltiplicato a sinistra per il vettore
è un bivettore, moltiplicato a sinistra per il vettore ![]() lo ruota (e scala) di
lo ruota (e scala) di ![]() in senso orario.
in senso orario.
Questo vettore costante è noto col nome di vettore di Laplace-Runge-Lenz, indicato con ![]() nella seguente figura. Come si vede, è costante e rivolto in direzione del periastro.
nella seguente figura. Come si vede, è costante e rivolto in direzione del periastro.
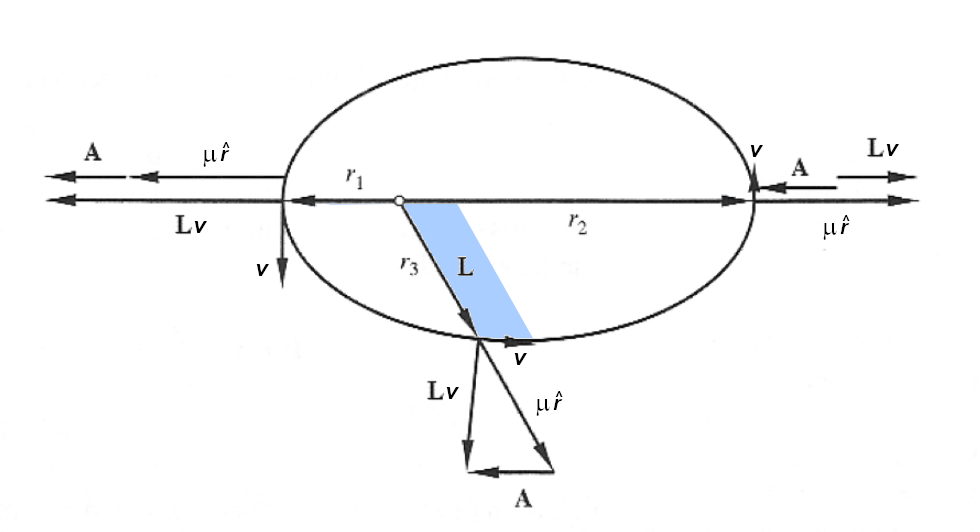
La traiettoria del pianeta
Elaboriamo questo interessante vettore costante moltiplicandolo a destra per il vettore ![]() :
:
![]()
Svolgendo tutti i i prodotti geometrici:
![]()
l’ultimo termine manca del wedge perché ![]() e
e ![]() hanno la stessa direzione.
hanno la stessa direzione.
Ricordando che ![]() :
:
![]()
Dal punto di vista dei gradi, questa equazione è composta da:
bivettore + scalare = scalare + bivettore + scalare
quindi andremo ad eguagliare i termini scalari (da notare: ![]() è positivo perché il quadrato di un bivettore è negativo!):
è positivo perché il quadrato di un bivettore è negativo!):
![]()
e riconosciamo l’equazione in forma polare ![]() :
:
![]()
molto simile all’equazione di una conica in forma polare, alla quale possiamo facilmente ricondurci:
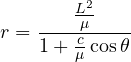
Ridefiniamo come ![]() (semilatus rectum) ed
(semilatus rectum) ed ![]() (eccentricità):
(eccentricità):
![]()
![]()
Ecco quindi svelata la traiettoria, con i principali parametri:
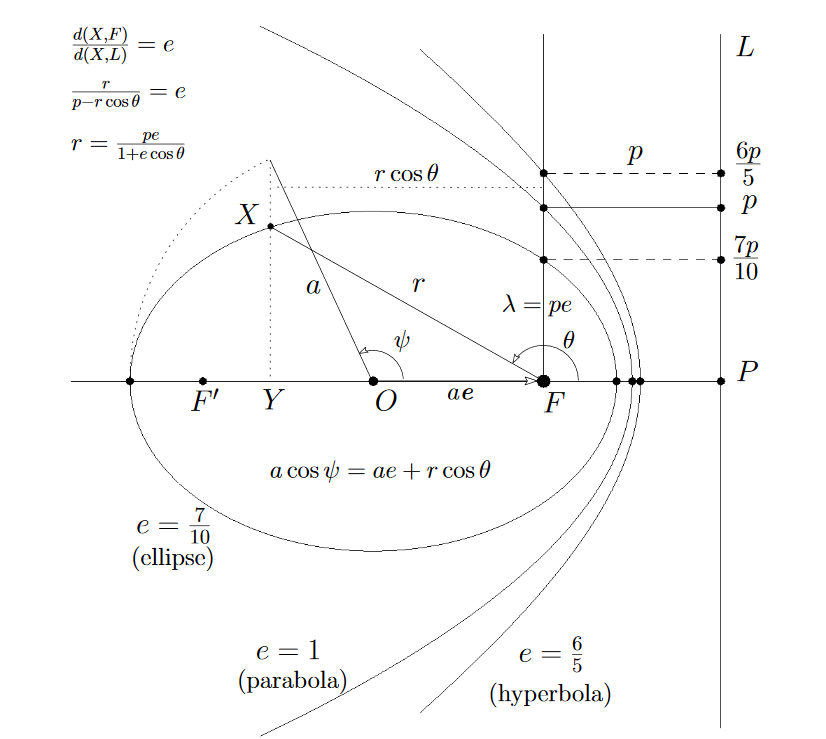
Adesso pensiamo al corpo ![]() in moto ellittico attorno ad
in moto ellittico attorno ad ![]() che occupa uno dei fuochi.
che occupa uno dei fuochi.
Esso descriverà il triangolo tratteggiato in un certo tempo e questo dipende dal momento angolare L perché abbiamo visto che
![]()

Nell’intero periodo orbitale ![]() descriverà l’area
descriverà l’area ![]() , ma quindi:
, ma quindi:
![]()
riorganizzando e passando ai quadrati:
![]()
e dalle proprietà geometriche dell’ellisse, sappiamo che ![]() e sappiamo anche che
e sappiamo anche che
![]()
e quindi:
![]()
semplificando e riorganizzando, otteniamo infine la terza legge di Keplero:
![]()
