Le equazioni di Maxwell – Algebra geometrica

Le equazioni di Maxwell ebbero una storia molto articolata, soprattutto perché man mano che si sviluppava la teoria dell’elettromagnetismo, si sviluppavano anche le tecniche matematiche utilizzate per descriverlo.

Nella prima pubblicazione del 1861-62, ancora intrisa di analogie meccaniche, Maxwell pubblicò queste 12 equazioni. Successivamente salirono a 20, ma queste includevano anche fenomeni (ad esempio la legge di Ohm) che oggi escludiamo dalle “fab four” equazioni di Maxwell.

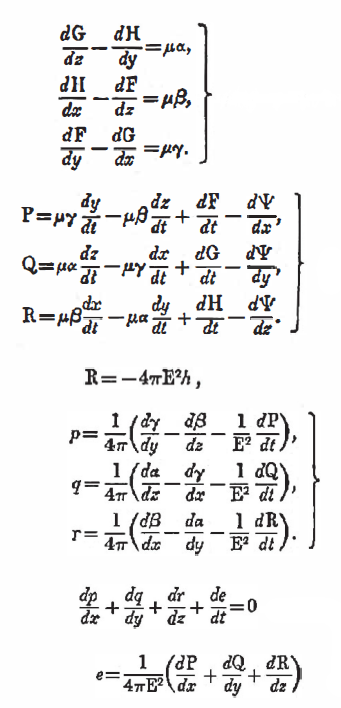
Poi, visto che erano la moda del momento, Maxwell tentò di riscriverle in forma di quaternioni, ma fu criticato dal suo pur entusiasta sostenitore Heaviside, che propose invece, insieme a Gibbs, una versione in forma vettoriale pura, rielaborata dai quaternioni, ma molto più efficace:
– niente somma di scalari e vettori (come erano concepiti i quaternioni da Hamilton)
– forma quadratica positiva
– moltiplicazione tra vettori in forma di prodotto scalare e vettoriale
– notazione in uso ancora oggi

$\begin{equation} \nabla \cdot \vec{E}} = \frac{\rho}{\epsilon_0}$
$\nabla \cdot \vec{B} = 0$
$\begin{equation} \nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}$
$\begin{equation} \nabla \times \vec{B} = \mu_0 \left ( J + \epsilon_0 \frac{\partial \vec{E}}{\partial t} \right )$

La rivoluzione della teoria della relatività, peraltro innescata dalle stesse equazioni di Maxwell che apparivano in forma covariante, cioè compatibile con i postulati della relatività, portarono però ad una loro riformulazione in forma di tensore.

E veniamo ora alla forma delle equazioni di Maxwell in chiave di AG. I tensori sono stati rimpiazzati dai bivettori ed i numeri complessi sono incorporati nella struttura dell’AG stessa.
Partiamo dagli ingredienti: le sorgenti del campo elettrico sono le cariche e le (densità di) correnti, condensate nel multivettore

$J = \rho - \pmb{J}$

dal punto di vista dimensionale, però, abbiamo un problema $[C][m]^{-3}$ vs $[C][s]^{-1}[m]^{-2}$ e rimediamo nel modo seguente:

$J = c \rho - \pmb{J}$

Poi il protagonista assoluto dell’elettromagnetismo: il campo elettromagnetico, come noto in AG vale $F = E + iB$ ma anche qui avremmo problemi dimensionali $[F][C]^{-1}$ vs $[F][C]^{-1}[v]^{-1}$ quindi lo modifichiamo in:

$F = E + icB$

Non è una modifica troppo traumatica: alcuni autori, tra i quali Gauss, hanno proposto di indicare il campo magnetico con l’espressione $cB$

Rullo di tamburi: le quattro equazioni di Maxwell diventano una sola:

$\begin{equation} \nabla F = \frac{1}{\epsilon_0 c}J$

Con la precisazione che l’operatore $\nabla$ va qui inteso in senso spazio-temporale, cioè:

$\begin{equation} \nabla = \frac{1}{c}\frac{\partial}{\partial t} + \frac{\partial}{\partial x} \hat{x} + \frac{\partial}{\partial y} \hat{y} + \frac{\partial}{\partial z} \hat{z}$

Questa equazione non ha solo il vantaggio della compattezza, ha soprattutto l’invarianza relativistica che deriva dall’aver moltiplicato per $c$ le quantità $\rho$ e $B$ .

Mostriamo ora come si possano derivare le ordinarie quattro equazioni di Maxwell.
Espandendo la definizione degli ingredienti visti sopra:

$\begin{equation} \left( \frac{1}{c}\frac{\partial}{\partial t} + \nabla \right ) (E + icB) = \frac{c \rho - J}{\epsilon_0 c}$

come secondo passo, distribuiamo il prodotto a sinistra:

$\begin{equation} \left( \frac{1}{c}\frac{\partial E}{\partial t} + \nabla E + i \frac{\partial B}{\partial t} + ic \nabla B \right ) = \frac{c \rho - J}{\epsilon_0 c}$

I due termini $\nabla E$ e $\nabla B$ si espandono ricordando il prodotto geometrico:
$\nabla \pmb{a} = \nabla \cdot \pmb{a} + \nabla \wedge \pmb{a}$

$\begin{equation} \frac{1}{c}\frac{\partial E}{\partial t} + \nabla \cdot E + \nabla \wedge E + i \frac{\partial B}{\partial t} + ic\: \nabla \cdot B + ic\: \nabla \wedge B = \frac{c \rho - J}{\epsilon_0 c}$

questa mostruosa equazione può essere riordinata nel modo seguente, con lo scopo di ordinare i termini per grado:

[NB: $ic\: \nabla \cdot B$ ha natura di trivettore perché viene moltiplicato per lo pseudoscalare i, mentre $ic\: \nabla \wedge B$ ha natura di vettore per lo stesso motivo!]

$\begin{equation} \underbrace{\nabla \cdot E}_\text{scalar} + \underbrace{\frac{1}{c}\frac{\partial E}{\partial t} + ic\: \nabla \wedge B}_\text{vector} + \underbrace{ \nabla \wedge E + i \frac{\partial B}{\partial t}}_\text{bivector} + \underbrace{ic\: \nabla \cdot B}_\text{trivector} = \frac{\rho}{\epsilon_0} - \frac{J}{\epsilon_0 c}$

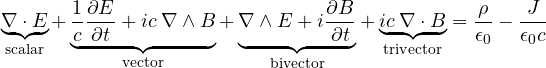
ora ci basta una semplicissima osservazione:
scalare + vettore + bivettore + trivettore = scalare + bivettore
dunque possiamo esprimere le relative uguaglianze per ogni grado

$\begin{equation} \nabla \cdot E = \frac{\rho}{\epsilon_0}$

$\begin{equation} \frac{1}{c}\frac{\partial E}{\partial t} + ic \nabla \wedge B = -\frac{J}{\epsilon_0 c}$

$\begin{equation} \nabla \wedge E + i \frac{\partial B}{\partial t} = 0$

$\begin{equation} ic \nabla \cdot B = 0$

La prima equazione, così com’è, esprime la legge di Gauss.

Per la seconda equazione c’è da lavorare un po’: innanzitutto dividiamola per $c$ , sapendo che $c^2 = \frac{1}{\epsilon_0 \mu_0}$ e richiamando in servizio il prodotto scalare $a \times b = i (a \wedge b)$ otterremo la forma:

$\begin{equation} \epsilon_0 \mu_0 \frac{\partial E}{\partial t} - \nabla \times B = - \mu_0 J$

a questo punto isoliamo il rotore di B ed otteniamo la legge di Ampère:

$\begin{equation} \nabla \times B = \mu_0 \left ( J + \epsilon_0 \frac{\partial E}{\partial t} \right )$

Anche nella terza equazione trasformiamo il prodotto esterno in quello vettoriale e separiamo E e B, ottenendo la legge di Faraday:

$\begin{equation} \nabla \times E = - \frac{\partial B}{\partial t}$

e l’utima equazione sarà semplicemente:

$\nabla \cdot B = 0$

… e ditemi che tutto questo non è meraviglioso!

Non solo: quanto abbiamo visto potrebbe sembrare un esercizio di stile, tanto bello quanto inutile.
Sembra che per fare i calcoli si debba tornare alle care vecchie equazioni: in realtà il prodotto geometrico ha potenza sufficiente per esprimere calcoli e l’eterea equazione $\nabla F = J$ può essere risolta con le funzioni di Green, per giunta in modo più facile!

Ad esempio se stiamo risolvendo un problema di elettrostatica in due dimensioni, quindi senza cariche all’interno della regione considerata, avremo $\nabla F = J$ e per mezzo delle funzioni di Green dovremo risolvere:

$\begin{equation} F(x) = \frac{1}{2 \pi i} \int_{\partial R} \frac{F(x')}{x'-x} dx'$

ovvero l’integrale di Cauchy.