Uno dei primi argomenti che si studiano nel corso di fisica è il moto del proiettile, che ha molti collegamenti con la realtà vissuta per esperienza diretta: dalle palle di neve ai calci di punizione. L’argomento si presta bene per riassumere la cinematica di un oggetto che si muove sotto l’influenza di un campo gravitazionale uniforme, che genera una accelerazione ![]() .
.
Per risolvere correttamente gli esercizi si impara il principio di sovrapposizione, che permette di separare i moti nelle direzioni orizzontale e verticale. Tipicamente gli esercizi chiedono di determinare il tempo di volo, la gittata, la velocità finale e anche di calcolare l’angolo di tiro che produce la gittata massima.
In questa pagina vediamo il tutto alla luce dell’algebra geometrica.
La situazione è quella classica: un proiettile viene sparato con una velocità iniziale rappresentata dal vettore ![]() che forma un angolo
che forma un angolo ![]() rispetto all’orizzontale. La posizione del proiettile in ogni istante è data dal vettore
rispetto all’orizzontale. La posizione del proiettile in ogni istante è data dal vettore ![]() .
.
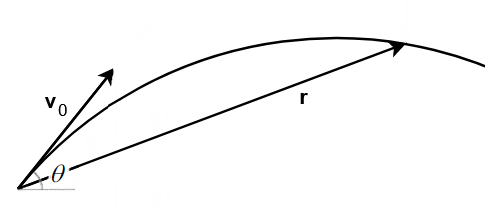
Il passo decisivo è dato dalla rappresentazione del diagramma delle velocità riferito ad un istante ![]() qualsiasi. Si parte dal vettore
qualsiasi. Si parte dal vettore ![]() e poi ci ricordiamo che agisce l’accelerazione di gravità
e poi ci ricordiamo che agisce l’accelerazione di gravità ![]() in senso verticale, quindi dalla punta di
in senso verticale, quindi dalla punta di ![]() parte un vettore rivolto verso il basso di modulo
parte un vettore rivolto verso il basso di modulo ![]() . La somma
. La somma ![]() produce il vettore velocità finale
produce il vettore velocità finale ![]() . Finora abbiamo tracciato un banalissimo triangolo.
. Finora abbiamo tracciato un banalissimo triangolo.
Adesso guardiamo il punto iniziale e quello dove si trova il proiettile nell’istante considerato ![]() : possiamo calcolare la velocità media e questa deve valere quanto lo spostamento totale
: possiamo calcolare la velocità media e questa deve valere quanto lo spostamento totale ![]() diviso il tempo totale
diviso il tempo totale ![]() , dunque:
, dunque:
![]()
ovvero ![]()
La nostra costruzione si è arricchita della somma di ![]() e
e ![]() , costituendo un parallelogramma valido per tutti gli istanti del moto:
, costituendo un parallelogramma valido per tutti gli istanti del moto:
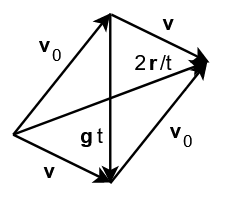
Da notare che è sufficiente variare ![]() ed il parallelogramma delle velocità si modificherà di conseguenza. Ad esempio (esercizi lasciati al lettore) possiamo ritrovare i casi classici della caduta dei gravi oppure del grave lanciato vero l’alto con velocità iniziale
ed il parallelogramma delle velocità si modificherà di conseguenza. Ad esempio (esercizi lasciati al lettore) possiamo ritrovare i casi classici della caduta dei gravi oppure del grave lanciato vero l’alto con velocità iniziale ![]() .
.
Vedremo che per risolvere tutti i problemi del moto dei proiettili è sufficiente risolvere questo parallelogramma elementare.
Prima il caso semplice: l’obiettivo da colpire si trova alla stessa quota del punto di partenza. Il parallelogramma in questo caso particolare dovrà avere la diagonale minore, che corrisponde al vettore posizione ![]() che giace sull’orizzontale.
che giace sull’orizzontale.
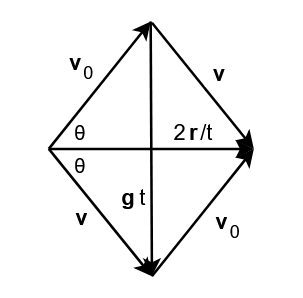
Osserviamo per via puramente geometrica che i vettori ![]() e
e ![]() sono uguali in modulo e simmetrici rispetto all’orizzontale. Vediamo ora i calcoli, richiamando le due proprietà che abbiamo costruito in precedenza:
sono uguali in modulo e simmetrici rispetto all’orizzontale. Vediamo ora i calcoli, richiamando le due proprietà che abbiamo costruito in precedenza:
![]()
![]()
e
![]()
Moltiplichiamole, per eliminare ![]() , ricordandoci che siamo in un mondo non-commutativo (quindi i due termini
, ricordandoci che siamo in un mondo non-commutativo (quindi i due termini ![]() non si cancellano!):
non si cancellano!):
![]()
![]()
richiamiamo in servizio l’utilissima identità che abbiamo visto trattando del prodotto geometrico a proposito del prodotto esterno: ![]()
Ricordiamoci, inoltre, che la moltiplicazione dei vettori ![]() e
e ![]() avviene con il prodotto geometrico.
avviene con il prodotto geometrico.
![]()
eguagliando i termini di pari grado (scalari con scalari e bivettori con bivettori) avremo:
![]()
![]()
Ma per come abbiamo costruito il problema ![]() perché sono perpendicolari, dunque la prima equazione ci dà un risultato interessante:
perché sono perpendicolari, dunque la prima equazione ci dà un risultato interessante: ![]() (c’entrerà qualcosa con la conservazione dell’energia?).
(c’entrerà qualcosa con la conservazione dell’energia?).
La seconda equazione riguarda le aree (ovviamente, essendo bivettori!) ma noi le sappiamo calcolare facilmente: se in modulo ![]() allora l’area del parallelogramma vale
allora l’area del parallelogramma vale ![]() e allora possiamo finalmente scrivere:
e allora possiamo finalmente scrivere:
![]()
e quindi la gittata vale
![]()
da qui la considerazione che, a parità di velocità iniziale, la gittata massima si ha per ![]() .
.
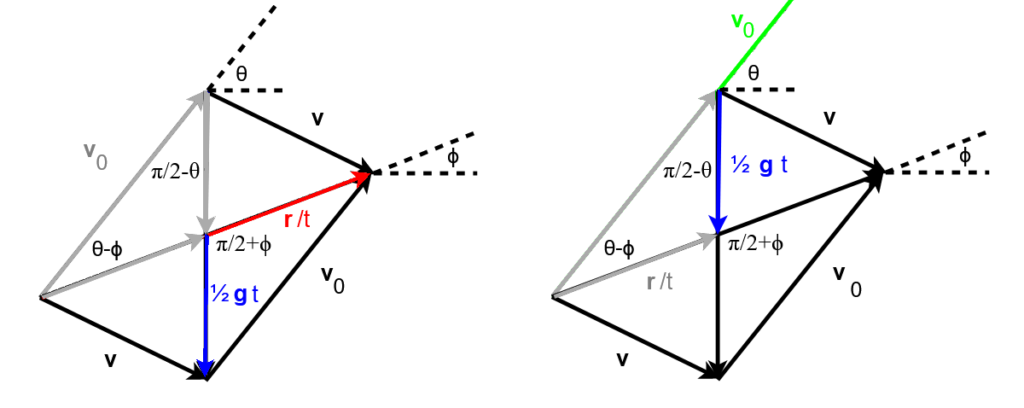
Adesso complichiamo le cose: l’obiettivo da colpire si trova ad una quota diversa, diciamo che si trova più in alto rispetto al punto di tiro. Il nostro parallelogramma, pensato per i punti iniziale e finale della traiettoria, sarà il seguente:
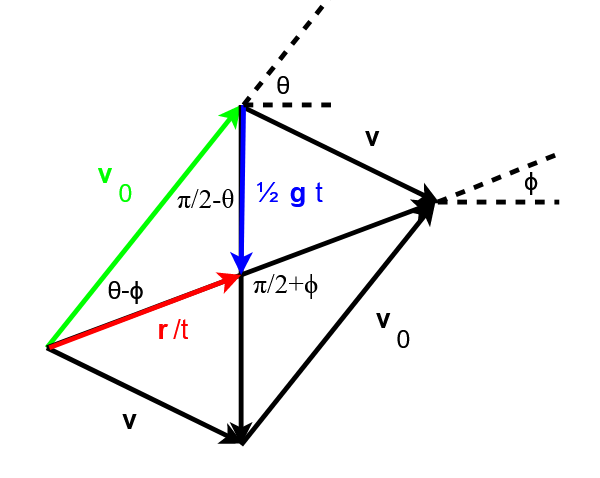
Di nuovo abbiamo l’angolo di tiro ![]() ed il nuovo angolo
ed il nuovo angolo ![]() che rappresenta l’angolo di elevazione dell’obiettivo visto dalla partenza. Da notare che – in ossequio alla geometria del parallelogramma – le diagonali si tagliano scambievolmente a metà e quindi i vettori rosso e blu valgono rispettivamente
che rappresenta l’angolo di elevazione dell’obiettivo visto dalla partenza. Da notare che – in ossequio alla geometria del parallelogramma – le diagonali si tagliano scambievolmente a metà e quindi i vettori rosso e blu valgono rispettivamente ![]() e
e ![]() .
.
La potenza dell’AG si esprime in modi molto elementari e ci fa toccare con mano che la fisica è geometria.
Concentrandoci sul triangolo colorato, possiamo vederlo come la metà di un parallelogramma e divertirci a determinarne l’area con i tre prodotti esterni fra i vettori colorati. Dovremo solo prestare attenzione a:
1) far partire i vettori dallo stesso punto
2) al verso del bivettore risultante (positivo in senso antiorario)
in questo modo:
![]()
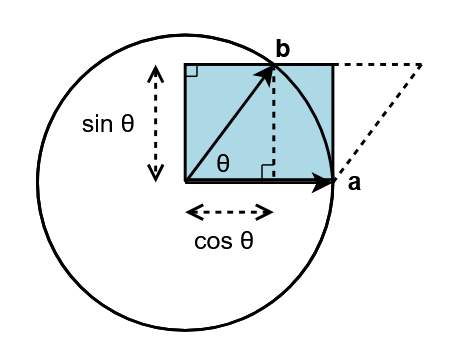
Se non fosse chiaro, il secondo ed il terzo wedge sono immaginati come segue:
Bene, svolto questo primo passo, applichiamo un altro principio importantissimo dell’AG: il fatto che il prodotto di due versori sia un rotore. Osservando di nuovo il parallelogramma con gli occhietti da rotore, quindi togliendo di mezzo i fattori di scala dei vettori coinvolti, possiamo scrivere queste uguaglianze:
![]()
![]()
![]()
Adesso ci ricordiamo della bellissima espressione vista nella pagina sui rotori:
![]()
e quindi possiamo dire che
![]()
![]()
![]()
Fermiamoci a riflettere su queste equazioni. Compare per la prima volta nei nostri calcoli l’unità immaginaria, ma abbiamo imparato a non allarmarci perché ora – grazie all’AG – la vediamo come un ente geometrico. L’unità immaginaria ![]() è una porzione unitaria di piano nel quale giace la nostra costruzione, ed è positivamente orientata in senso antiorario. Nulla di più di questo.
è una porzione unitaria di piano nel quale giace la nostra costruzione, ed è positivamente orientata in senso antiorario. Nulla di più di questo.
Se ![]() è la torta,
è la torta, ![]() è una fetta (orientata) di questa torta.
è una fetta (orientata) di questa torta.
Ora abbiamo davvero tutti gli ingredienti per i nostri calcoli.
Riscriviamo le uguaglianze tra i prodotti esterni in modo da lasciare evidenziati i versori:
![]()
allora ricaviamo facilmente il tempo di volo dalle prime due espressioni:
![]()
e dalle ultime due, ora che conosciamo ![]() , possiamo ricavare la distanza
, possiamo ricavare la distanza ![]() :
:
![]()
Da notare che questo risultato, con la tecnica classica in coordinate rettangolari (American Journal of Physics 47, 466), richiede calcoli molto più complessi.
Incidentalmente, notiamo che possiamo richiamare uno dei risultati ottenuti per il caso iniziale:
![]()
e riconosciamo in questa espressione il principio di conservazione dell’energia, ovvero che la perdita di energia cinetica è pari all’incremento dell’energia potenziale del proiettile.
Il senso di tutto questo, al di là delle formule finali è: la fisica è essenzialmente geometria e l’algebra geometrica rende le cose molto più semplici.
