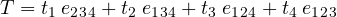Alcuni testi di fisica accanto ai vettori classici (detti anche polari) introducono i vettori assiali, detti anche pseudovettori e sono definiti come quei vettori che manifestano i loro effetti fisici in un piano ad essi perpendicolare.
Esempi tipici sono la velocità angolare e la coppia.
L’aspetto singolare è che non vi è alcuna differenza di notazione: vengono indicati allo stesso modo pur avendo un comportamento radicalmente diverso.
J.D. Jackson nel suo “Classical electrodynamics” fa notare “We see here . . . a dangerous aspect of our usual notation. The writing of a vector as ‘a’ does not tell us whether it is a polar or an axial vector’’.
… per amor di completezza, riportiamo che i francesi sono soliti indicare i vettori assiali sovrapponendo alla lettera una freccetta curva:
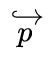
Come facciamo a distinguere tra un vettore normale ed uno assiale? Allo stesso modo con cui distinguiamo i vampiri dalle persone normali: con uno specchio.
Se una pallina è in moto in direzione perpendicolare allo specchio, guardando la sua immagine riflessa la vedremo muoversi in direzione opposta, quindi possiamo dire che lo specchio inverte il vettore velocità.
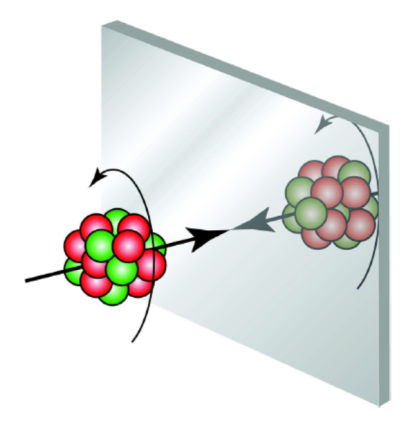
Se invece la pallina sta ruotando in senso antiorario davanti allo specchio, anche la sua immagine ruoterà nello stesso senso. Il vettore assiale ![]() (velocità angolare), come i vampiri, NON si riflette nello specchio.
(velocità angolare), come i vampiri, NON si riflette nello specchio.
Scherzi a parte, questo è un caso lampante di come la fisica classica abbia bisogno di modificare alcune sue definizioni di base. E’ del tutto evidente che i vettori assiali siano in realtà dei bivettori.
- i vettori assiali nascono da un prodotto vettoriale o da un rotore di un campo vettoriale
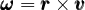
i bivettori nascono da un prodotto esterno che, come abbiamo visto, è il duale del prodotto vettoriale
- i vettori assiali sotto inversione spaziale (
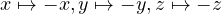 ) rimangono invariati:
) rimangono invariati: 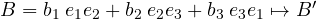
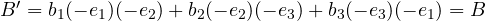
- i vettori assiali sono chiusi rispetto alla somma (come i bivettori) ma la somma di un vettore polare con uno assiale risulta un’entità che si può ancora definire vettore secondo la fisica, ma non rispetta le regole sull’inversione spaziale. La violazione della simmetria CP a livello nucleare può essere ricondotta alla somma di un vettore assiale (lo spin) con un vettore
- in uno spazio di dimensione
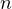 si comportano come pseudovettori gli elementi di ordine
si comportano come pseudovettori gli elementi di ordine  (che hanno
(che hanno 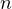 basi, ognuna delle quali è formata dal prodotto esterno di tutte le basi tranne una).
basi, ognuna delle quali è formata dal prodotto esterno di tutte le basi tranne una).
Ad esempio, in 4 dimensioni gli pseudovettori sono i trivettori