Abbiamo visto che se prendiamo un vettore ![]() e lo riflettiamo rispetto al vettore
e lo riflettiamo rispetto al vettore ![]() e poi al vettore
e poi al vettore ![]() (in questo ordine) otteniamo una rotazione del vettore di un angolo doppio rispetto a quello tra
(in questo ordine) otteniamo una rotazione del vettore di un angolo doppio rispetto a quello tra ![]() e
e ![]() (in questo ordine).
(in questo ordine).
Algebricamente si tratta di applicare due volte la riflessione rispetto ad un vettore, col noto prodotto a sandwich: ![]()
Quindi se vogliamo una rotazione pari ad ![]() dovremo utilizzare un rotore
dovremo utilizzare un rotore ![]() che fu chiamato spinore da Wolfgang Pauli per il motivo che vedremo a breve.
che fu chiamato spinore da Wolfgang Pauli per il motivo che vedremo a breve.
Dunque abbiamo questa strana uguaglianza:
![]()
dalla quale deduciamo che le due rotazioni ![]() e
e ![]() rappresentano la stessa rotazione ma in due direzioni opposte:
rappresentano la stessa rotazione ma in due direzioni opposte:
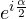 rappresenta la rotazione antioraria nell’intervallo
rappresenta la rotazione antioraria nell’intervallo ![Rendered by QuickLaTeX.com \alpha\in[0;2\pi]](https://geometrica.vialattea.net/wp-content/ql-cache/quicklatex.com-9d5264ffda3621adbb9d66eb29273a0f_l3.png)
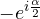 rappresenta la rotazione oraria nell’intervallo
rappresenta la rotazione oraria nell’intervallo ![Rendered by QuickLaTeX.com \alpha\in[2\pi;4\pi]](https://geometrica.vialattea.net/wp-content/ql-cache/quicklatex.com-3aa441d32dcfb425d0a5163414695df3_l3.png) dato che:
dato che: 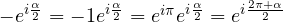
Ma ![]() e quindi gli spinori hanno periodicità
e quindi gli spinori hanno periodicità ![]() !
!
Se gli spinori vi sembrano strani … è perché lo sono!!
E’ scolpito nelle convinzioni di ognuno che un oggetto ritorni allo stato iniziale dopo una rotazione di ![]() , ma stavolta abbiamo a che fare con con oggetto che torna se stesso dopo due rotazioni.
, ma stavolta abbiamo a che fare con con oggetto che torna se stesso dopo due rotazioni.
La faccenda può essere mostrata col trucco di Dirac del piattino oppure della cintura, che lascerà sbalorditi gli spettatori come se fosse uno spettacolo di magia.
Questo fatto rende un po’ meno strano lo spin semi-intero degli elettroni.
