Gli elementi di grado uno, vale a dire i vettori, si sommano con la classica regola del parallelogramma, ovvero si sommano algebricamente le componenti.
Per gli elementi di grado due, ovvero i bivettori, occorre procedere con più cautela.
Un bivettore è una porzione orientata di piano, quindi è caratterizzata da una grandezza (la misura dell’area) da un verso (dato dalla circuitazione) e dall’orientazione nello spazio. Sembra sorprendente, ma il bivettore non ha forma!
Infatti può essere pensato come un rettangolo oppure un cerchio o qualsiasi altra forma, il che ci risulta utile per la somma.
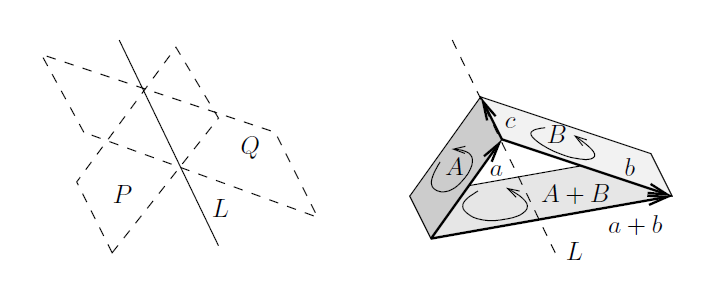
Immaginiamo di dover sommare due bivettori A e B, che giacciono su due piani P e Q che si incontrano lungo la linea L.
Possiamo modificare la forma di A e B in modo che siano generati da un vettore comune 
, quindi:
Risulterà quindi
Accanto al concetto di somma possiamo vedere quello di proiezione di un bivettore nelle sue componenti, aiutandoci col seguente box interattivo, dalla pagina di Marc ten Bosch.
Il prodotto esterno dei due vettori 
e 
genera un bivettore nello spazio tridimensionale (in blu). Questo può essere proiettato nei piani fondamentali ottenendo i tre bivettori componenti (in arancio, viola e giallo).
Provate a spostare i punti a e b ed osservate come variano le proiezioni. Le componenti dei vettori possono essere fissate scrivendole direttamente nei box bianchi. E’ anche possibile ruotare il punto di vista per capire meglio le relazioni geometriche tra gli elementi.
Ricordando i prodotti esterni dei versori:
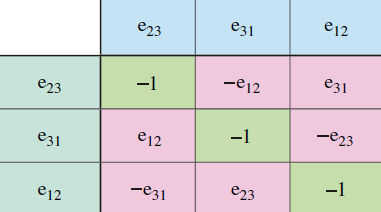
otterremo finalmente che il bivettore blu 
ha come componenti:
Esercizio: verificare che 