Apriamo una digressione estremamente affascinante, che spiega l’onnipresenza della funzione esponenziale ![]() in questa trattazione. Infatti abbiamo determinato che il generatore delle rotazioni 2D è il bivettore unitario
in questa trattazione. Infatti abbiamo determinato che il generatore delle rotazioni 2D è il bivettore unitario ![]() ed infatti moltiplicandolo per un qualsiasi vettore, lo ruota di
ed infatti moltiplicandolo per un qualsiasi vettore, lo ruota di ![]() .
.
Se volessimo una rotazione dimezzata, tuttavia, non potremmo semplicemente moltiplicarlo per ![]() . L’espressione corretta passa per la funzione esponenziale, che definisce correttamente il rotore. Questo risulta l’unico modo per trasferire la linearità nella rotazione.
. L’espressione corretta passa per la funzione esponenziale, che definisce correttamente il rotore. Questo risulta l’unico modo per trasferire la linearità nella rotazione.
Partiamo da una domanda talmente semplice da risultare infantile: come vengono generati tutti i numeri?
La prima risposta che viene in mente arriva proprio dall’infanzia: abbiamo imparato a contare sulla punta delle dita e quindi i numeri vengono generati per accumulazione dallo zero a passi di uno. Ad esempio per generare il numero 8 ci servono otto passi.
La seconda risposta ci viene insegnata qualche anno dopo, con le tabelline. I numeri possono essere generati per moltiplicazione, immaginata come una sequenza di addizioni controllata da un contatore.
Ad esempio si arriva all’8 accumulando la quantità due per quattro volte, oppure la quantità quattro per due volte.
Alla fine delle elementari si impara anche il concetto di potenza che, in modo analogo, è una sequenza di moltiplicazioni della base controllata da un contatore (esponente).
Tutte queste modalità funzionano, ma prevedono sempre una specie di algoritmo che dall’esterno controlla il compiersi di un processo. L’aggettivo “naturale” nel titolo della pagina dice che vogliamo trovare un processo il più possibile semplice ed autoesplicativo, che scaturisce da se stesso, senza meccanismi esterni. Questo processo esiste ed è la crescita.
Inoltre nei processi che abbiamo elencato ci sono dei buchi difficili da colmare.
Ad esempio come spieghiamo l’espressione ![]() o l’espressione mistica
o l’espressione mistica ![]() o addirittura
o addirittura ![]() ?
?
La crescita
Partiamo dall’origine filosofica di tutti i numeri: l’unità.
Adesso immaginiamo che ci sia un processo di crescita che in una unità di tempo porti l’unità ad aumentare di un fattore ![]() :
:
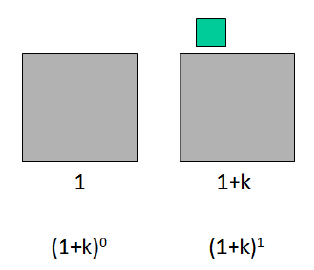
Il passo successivo è interessante perché non vede soltanto la generazione di un’altra frazione ![]() : si aggiunge un’altra frazione
: si aggiunge un’altra frazione ![]() figlia della crescita precedente. Questo avviene perché nella nostra crescita naturale tutte le parti sono attive nel processo.
figlia della crescita precedente. Questo avviene perché nella nostra crescita naturale tutte le parti sono attive nel processo.

Quindi il terzo passo vedrà ogni oggetto generare una frazione k-esima di se stesso
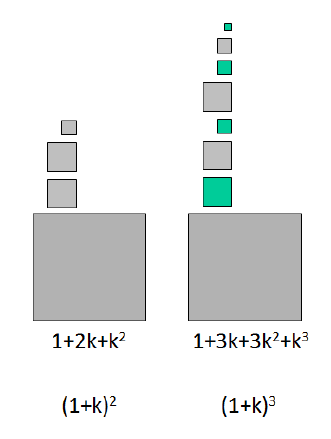
Lo schema ormai è ben visibile:

In ogni passo il numero di p-elementi (quelli scalati p volte, cioè che misurano ![]() ) è dato da quelli presenti al passo precedente più il numero di elementi padre, ovvero quelli
) è dato da quelli presenti al passo precedente più il numero di elementi padre, ovvero quelli ![]() , secondo il triangolo di Pascal:
, secondo il triangolo di Pascal:

Infatti possiamo scrivere ogni riga del triangolo di Pascal come somma della precedente ed una versione scalata di un passo.

E’ interessante notare che questo processo è auto-simile: la porzione nuova che si genera al passo ![]() è ciò che esisteva al passo precedente scalata di
è ciò che esisteva al passo precedente scalata di ![]() .
.
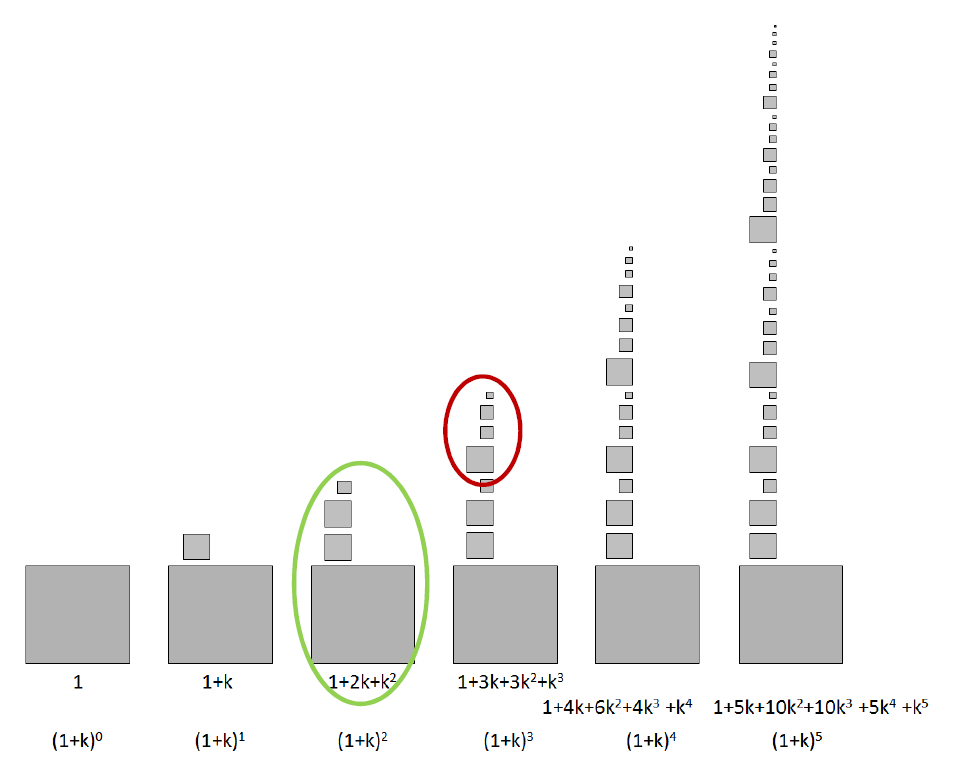
Dopo questa premessa, entriamo nel vivo della questione: vogliamo esplorare la proprietà del processo di crescita naturale con k=1, ovvero ad ogni passo la quantità genera una copia di se stessa. La assumiamo come espressione di crescita naturale perché ci fa venire in mente l’accrescimento di un tessuto per divisione cellulare.
Se questo processo avvenisse in un singolo passo, avremmo una crescita di 1 per un totale di 2.
Se il processo avvenisse in due passi di ampiezza 1/2 allora la crescita sarebbe proporzionale alla frazione 1/2 e per il totale potremo usare l’espressione ![]()
Se i passi fossero tre: ![]()
Con cento passi avremmo una buona approssimazione di cosa significa il raddoppio naturale continuo:![]()
E’ interessante verificare che il limite per un numero infinito di passi è una quantità finita e definisce uno dei numeri più importanti:
![]()
Se invece di un raddoppio fosse una triplicazione? L’espressione del totale andrebbe modificata in questo modo:
![]()
Insomma l’esponenziazione che abbiamo imparato alle scuole elementari può essere vista come un caso particolare di un processo di crescita continua nel quale ogni elemento ne genera altri, che sono parte attiva nel processo. Non pensiamo più ai numeri come sassolini da accumulare o dividere ma piuttosto ad un fluido che si espande continuamente in tutte le sue parti infinitesime.
Ricapitolando, il nostro modello mentale usa tre parametri:
– la quantità iniziale A che possiamo fissare all’unità, in grado di generare tutti i numeri
– il fattore di crescita k, che possiamo fissare ad 1 (il raddoppio)
– il tempo, che rimane a tutti gli effetti il parametro libero
La quantità finale sarà ![]()
Per la proprietà di auto-somiglianza di cui abbiamo parlato in precedenza, ogni porzione della curva è uguale alla curva stessa. In particolare, dato che ![]() la sua derivata è pari al valore della funzione stessa, essendo:
la sua derivata è pari al valore della funzione stessa, essendo:
![]()
Inoltre, si vede bene che il valore al passo ![]() è pari alla somma di tutti gli incrementi dei passi precedenti, dal momento che per il teorema fondamentale del calcolo integrale:
è pari alla somma di tutti gli incrementi dei passi precedenti, dal momento che per il teorema fondamentale del calcolo integrale:
![]()
ma abbiamo appena mostrato che ![]() e quindi abbiamo
e quindi abbiamo
![]()
Quindi possiamo dire che per la straordinaria funzione di crescita naturale il presente coincide col futuro (l’incremento) e col passato (il valore cumulato).
Possiamo applicare gli stessi ragionamenti con ![]() che è un numero negativo, ovvero una erosione continua dell’unità. La formula della quantità finale resterebbe valida ed otterremmo che la successione converge al valore
che è un numero negativo, ovvero una erosione continua dell’unità. La formula della quantità finale resterebbe valida ed otterremmo che la successione converge al valore ![]() .
.
Tornando al nostro problema iniziale di spiegare come vengono generati tutti i numeri, abbiamo ottenuto una formula che ci permette di ottenere tutti i numeri maggiori di zero, ma non lo zero e nemmeno i numeri negativi.
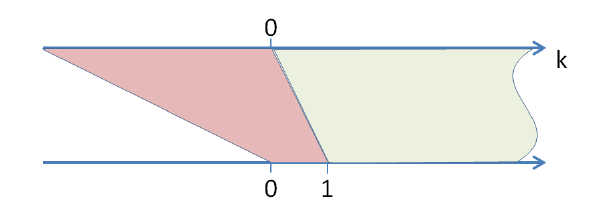
Quindi rimane il problema di generare in modo naturale i numeri negativi e – già che ci siamo – spiegare perché ![]() e aumentando di uno l’esponente l’intera espressione cambia segno:
e aumentando di uno l’esponente l’intera espressione cambia segno: ![]()
La crescita immaginaria
Quanto abbiamo visto può essere esteso alla forma immaginaria come segue: l’unità cresce di una quantità immaginaria ![]() e genera la seguente sequenza:
e genera la seguente sequenza:

che possiamo rappresentare come nel caso precedente, ma con l’accorgimento di colorare in arancio i termini immaginari, disponendoli a sinistra (positivi) o a destra (negativi). Anche qui una (quasi) auto-somiglianza, perché dobbiamo moltiplicare ogni blocchetto del passo precedente per ![]() .
.
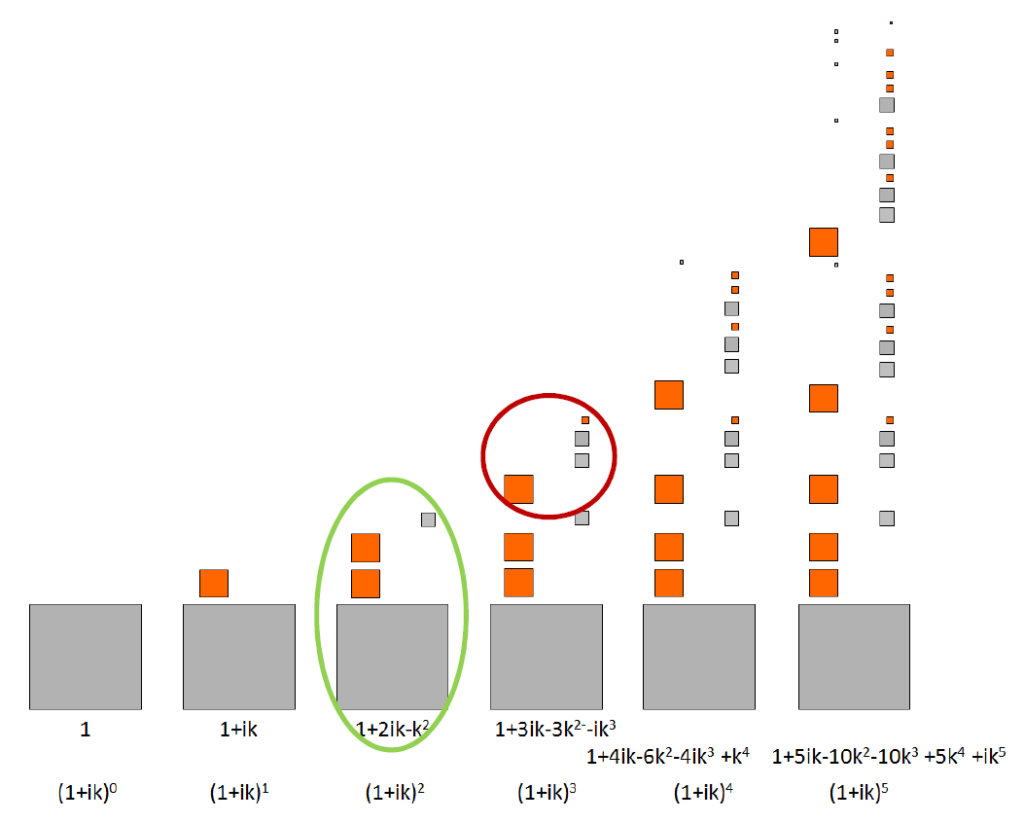
Questa visualizzazione però è troppo complicata e non ci aiuta: meglio ricorrere al piano di Argand-Gauss, dove i quadratini grigio e arancio diventano le componenti reali ed immaginarie di una sequenza di punti.
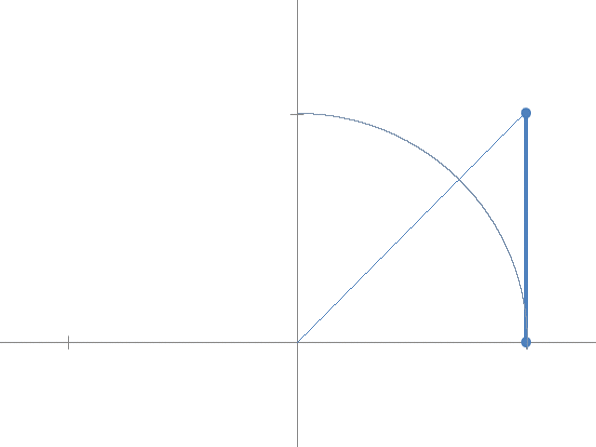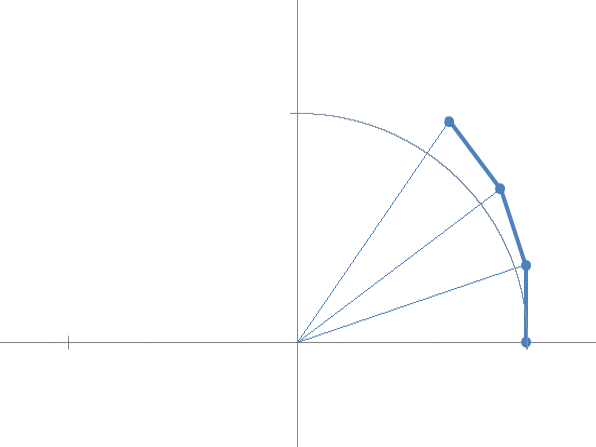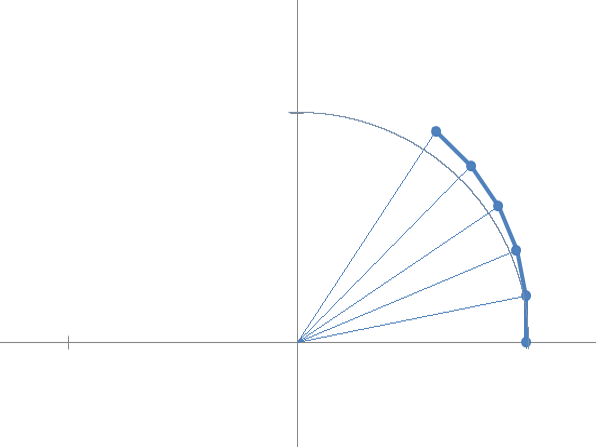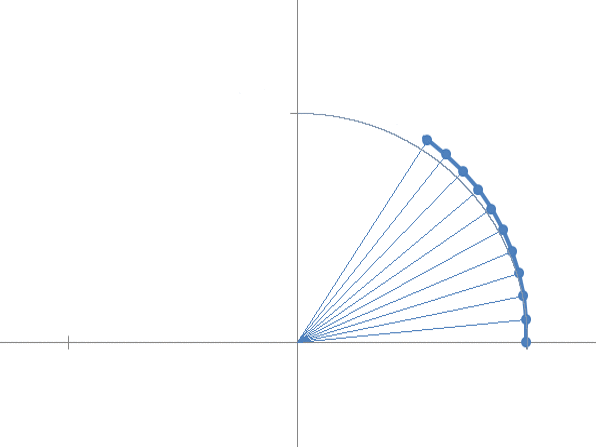
Diciamo che ![]() e osserviamo la crescita in tre passi:
e osserviamo la crescita in tre passi:

Il primo passo definisce un triangolo rettangolo con cateto maggiore 1 e cateto minore ![]() la loro somma è ovviamente l’ipotenusa.
la loro somma è ovviamente l’ipotenusa.
I passi successivi sono legati al primo dalla relazione di auto-somiglianza, quindi il secondo triangolo partirà dall’ipotenusa del primo al quale si sommerà una versione scalata per ![]() di se stesso.
di se stesso.
Questo ha una interessante implicazione: in tutti i passi l’angolo al centro è lo stesso.
Ora immaginando di passare al continuo, aumentiamo i passi ed osserviamo che il limite della successione si trova sulla circonferenza unitaria e definisce un arco di ampiezza unitaria (in radianti).
Se ora aumentiamo il fattore di accrescimento ![]() , scopriamo che la successione converge ad un valore che si trova sempre sulla circonferenza unitaria ma descrivendo un arco di ampiezza 2 radianti.
, scopriamo che la successione converge ad un valore che si trova sempre sulla circonferenza unitaria ma descrivendo un arco di ampiezza 2 radianti.
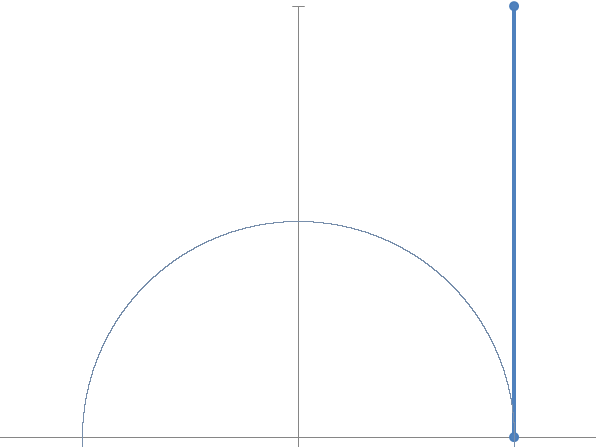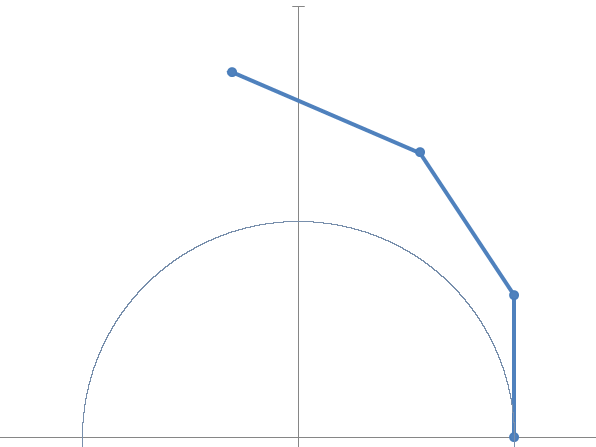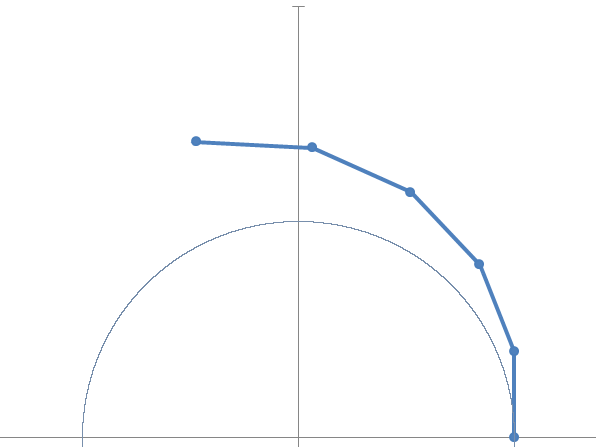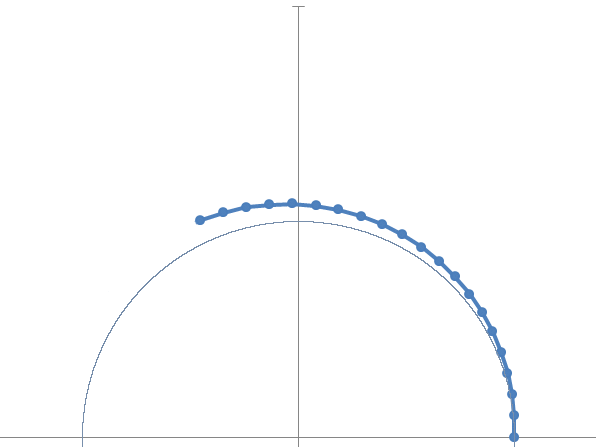
Quindi possiamo interpretare l’espressione della crescita immaginaria con l’equivalenza simbolica:
![]()
e la “mistica” formula di Eulero può essere interpretata come il caso particolare di un processo di crescita immaginaria continua. Se il fattore di crescita è ![]() , porta il numero 1 a mapparsi sul numero -1, ovvero a ruotare di
, porta il numero 1 a mapparsi sul numero -1, ovvero a ruotare di ![]() radianti.
radianti.
La sintesi
Per riassumere, abbiamo trovato il modo di generare nel modo più naturale possibile tutti i numeri a partire dall’unità per mezzo della stessa struttura esponenziale ![]() .
.
Se ![]() è reale positivo, si tratta di una crescita, se reale negativo è una contrazione, se è immaginario sarà una rotazione di
è reale positivo, si tratta di una crescita, se reale negativo è una contrazione, se è immaginario sarà una rotazione di ![]() radianti. Per la proprietà delle potenze, possiamo combinare i due effetti nell’esponente complesso:
radianti. Per la proprietà delle potenze, possiamo combinare i due effetti nell’esponente complesso:
![]()
che esprime in una sola operazione la trasformazione fondamentale in grado di generare tutti i numeri: scalare e ruotare l’unità.
