We have seen that if we take a vector ![]() and reflect it with respect to the vector
and reflect it with respect to the vector ![]() and then to the vector
and then to the vector ![]() (in this order) we obtain a rotation of the vector of an angle double the one between
(in this order) we obtain a rotation of the vector of an angle double the one between ![]() and
and ![]() (in that order).
(in that order).
Algebraically it is a question of applying reflection twice with respect to a vector, with the known sandwich product: ![]()
So if we want a rotation equal to ![]() we will have to use a rotor
we will have to use a rotor ![]() which was named spinor by Wolfgang Pauli for the reason that we will see shortly.
which was named spinor by Wolfgang Pauli for the reason that we will see shortly.
So we have this strange equality:
![]()
from which we deduce that the two rotations ![]() e
e ![]() represent the same rotation but in two opposite directions:
represent the same rotation but in two opposite directions:
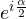 represents the counter-clockwise rotation in the range
represents the counter-clockwise rotation in the range ![Rendered by QuickLaTeX.com \alpha\in[0;2\pi]](https://geometrica.vialattea.net/wp-content/ql-cache/quicklatex.com-9d5264ffda3621adbb9d66eb29273a0f_l3.png)
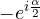 represents the clockwise rotation in the interval
represents the clockwise rotation in the interval ![Rendered by QuickLaTeX.com \alpha\in[2\pi;4\pi]](https://geometrica.vialattea.net/wp-content/ql-cache/quicklatex.com-3aa441d32dcfb425d0a5163414695df3_l3.png) given that:
given that: 
But ![]() so spinors have a
so spinors have a ![]() period !
period !
If spinors seem strange to you … it is because they are!
It is carved into everyone’s beliefs that an object returns to its initial state after a rotation of ![]() , but this time we are dealing with an object that returns to itself after two rotations.
, but this time we are dealing with an object that returns to itself after two rotations.
This weirdness can be demonstrated with Dirac’s trick of the saucer or the belt, which will leave the spectators astounded as if it were a magic show.
This makes the half-integer spin of electrons a little less strange, after all.
