The duality

The concept of duality in physics is extremely interesting because it connects aspects that can be considered opposites , by means of a correspondence which instead it leads to identify oneself in the formal aspect, or in the equations.
In this sense, duality is the best translation of the suggestive concept of coincidentia oppositorum of the medieval philosophical tradition.

In physics, duality is largely found in electrical phenomena:

• voltage – current
• circuit series – circuit parallel
• resistance 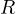– conductance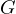
• voltage divider – current divider
• impedance 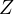– admittance
• capacity 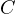– inductance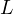
• reactance 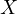– susceptance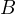
• short circuit – open circuit
• Kirchhoff’s current law at a node – Kirchhoff’s voltage law in a loop
• Thévenin’s theorem – Norton’s theorem

Far from being confined to circuits, the principle of duality is one of the unifying ideas of modern physics. The philosophers of physics De Haro and Butterfield have even described a duality as “a giant symmetry”: a correspondence so deep that it identifies two seemingly different descriptions of the same phenomenon. Some famous examples:

• electric ↔ magnetic: the symmetry of Maxwell’s equations in vacuum;
• position ↔ momentum: in quantum mechanics, linked by the Fourier transform;
• wave ↔ particle: the duality at the heart of quantum physics;
• order ↔ disorder (Kramers-Wannier): linking high and low temperatures in statistical mechanics;

In all these cases we find the same structure: two opposite faces that the equations reveal to be one and the same thing — the coincidentia oppositorum we spoke of at the beginning.

In addition to a speculative interest, the principle of duality has a practical implication much loved by students because it allows you to memorize only half of the formulas, because the dual ones are immediately obtainable. For example the capacitor is characterized by this constitutive relationship:

knowing that inductance is the dual quantity of capacitance and that voltage and current are also dual quantities, the dual relation is immediately obtained:

Finally the principle of duality is a heuristic principle, that is, it serves to discover something new.
In 1825 the French mathematician Joseph Gergonne noticed that for every theorem in projective geometry that involved lines and points, a dual one corresponded, that is, obtained by exchanging the roles of lines and points. For example to the 2D theorem “two points define a line” corresponds “two lines meet at a point” and to the 3D theorem “three points define a plane” corresponds “three planes intersect at a point”.

In algebra the notion of duality corresponds to the orthogonal complement , i.e. the subspace formed by all the bases that do not constitute the element.

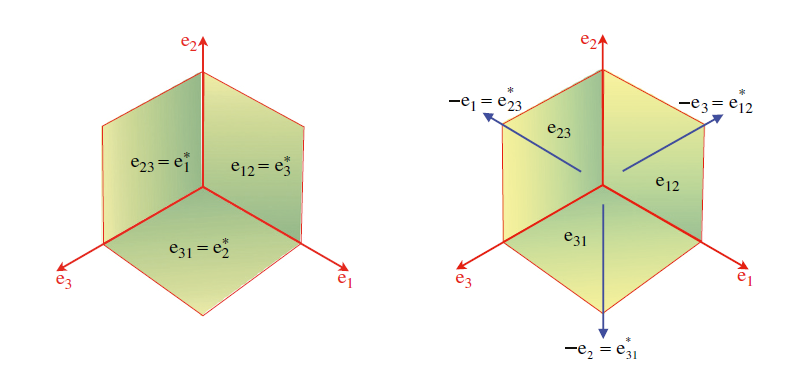
The duality relation is so important in GA that it has its own dedicated symbol, the asterisk $^*$ (star). The dual of a multivector is obtained by multiplying by the unit pseudoscalar. Here, however, a question of convention arises: consistently with the conventions page, we adopt multiplication on the right by the *inverse* of the pseudoscalar,$$M^* = M\,I^{-1}$$the definition used by Hestenes and by A. MacDonald (see references). Other authors, for instance Doran in [7], define the dual as $M^* = MI$. Note carefully: the two definitions are not equivalent, because in 3D we have $I^{-1} = -I$ and therefore $MI^{-1} = -MI$: the two duals differ by a sign.
It is precisely this freedom of convention (right or left, with $I$ or with $I^{-1}$) that is the reason why a sign “always seems to wobble” in the dual. Once the convention $M^* = MI^{-1}$ is fixed, however, the sign is settled once and for all.

For example, the dual of the plane identified by the bases

If instead we start from the vector we will have to use the inverse transformation and therefore

therefore it is necessary to pay attention to the direction in which we are carrying out the duality operation: from vectors to bivectors or the other way around.

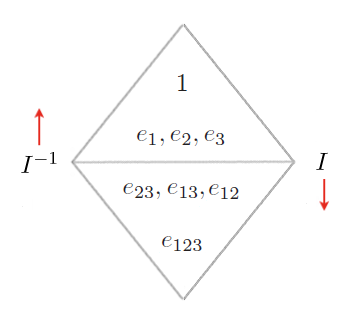
It is interesting to note that where , therefore in 2D and 3D, the dual of the dual of an element does not coincide with the element itself: there is a minus sign to make the difference. For example


therefore it takes two cycles of duality to bring us back to the original element.
In general in a n-dimension space we will have .

The duality relation has been used unconsciously for decades in vector algebra: in fact the phantom axial vectors are nothing more than masked bivectors, as can be seen in the figure

As an exercise, we calculate the dual of the external product :

since in 3D the pseudoscalar I switches with each element. Therefore, by carrying out:

We recognize the classic vector product in the final expression!
Therefore between the external product and the vector product there is a relationship of duality.
The inverse relationship also holds:

It is worth emphasizing a difference between the dual of a multivector and its orthogonal complement. The difference is subtle but important. The orthogonal complement of a plane is the line perpendicular to it: a subspace, that is, a set of directions, with no length and no orientation. The dual of that plane, instead, is a definite vector, with a magnitude (proportional to the area of the plane) and an orientation (consistent with that of the plane). In other words: the orthogonal complement tells you where the dual object lies, but it is duality that tells you how big it is and which way it points.

There is a remarkable consequence in all this. The notorious “right-hand rule” — the bane of every physics student — is not a law of nature: it is simply the choice of orientation of the pseudoscalar. All the arbitrariness of “handedness” is concentrated in a single spot, the sign of $I$ (choosing $I = e_1e_2e_3$​ rather than $e_3e_2e_1$​ amounts to declaring the basis triple right-handed).

This is clear once we decompose the cross product $\pmb{a}\times\pmb{b} = (\pmb{a}\wedge\pmb{b})\,I^{-1}$: the bivector $\pmb{a}\wedge\pmb{b}$ is a wholly intrinsic object, an oriented area in its own plane, which “knows” nothing of right or left. Chirality enters the stage only when we multiply by $I$ to obtain the axial vector: it is there, and only there, that we must decide “on which side of the plane” the axis points. Flip the orientation of $I$ and the cross product reverses — but the bivector stays the same.

In other words, the right-hand rule is a property of the dual (the device that disguises a bivector as a vector), not of the underlying geometry. Working directly with bivectors, as we saw when discussing axial vectors, the problem simply vanishes: no hand required.