The well-known vectors and even subalgebra, which we have called generalized complex numbers, are two subsets of 2D geometric algebra.
What interactions exist between these two worlds? We find out with these simple test calculations.
We take two vectors as representatives of the odd degree of ![]() :
:
![]()
![]()
their linear combination ![]() generates the vector space
generates the vector space ![]() which we represent with a plane. We then have two more elements, this time members of
which we represent with a plane. We then have two more elements, this time members of ![]() :
:
![]()
![]()
they too by linear combination ![]() generate a subspace of
generate a subspace of ![]() that we can represent with a plane. Now let’s see what happens when we multiply these elements together:
that we can represent with a plane. Now let’s see what happens when we multiply these elements together:
![]()
![]()
![]()
So the product of two vectors – as we have already seen – generates a complex number. If the vectors are unitary, this complex number takes the name of rotor because it is able to operate a rotation on a vector without altering its modulus, which we see immediately:
![]()
![]()
![]()
The result, therefore, is still a vector. It is not very clear what happened, just by looking at the algebra of the coefficients. Much clearer if we see it in action on the plane by drawing the vectors.
Finally, let’s look at what happens when two complex numbers are multiplied:
![]()
which is still a complex number in which we can see one rotated from the other or vice versa.
So, summing up, here are the interactions between vectors and complex numbers:
| · | ||
rotated by scaled by | ||
rotated by scaled by |
It should be clear that it is wrong to identify complex numbers as vectors, despite both being representable on a plane, for several reasons.
- in the vector plane the symmetry is broken by the two privileged directions
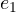 and
and 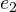 , while in the plane of complex numbers there is only one privileged direction: that of the
, while in the plane of complex numbers there is only one privileged direction: that of the 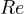 axis, while there is total rotational freedom (the bivector, by its nature, does not identify a direction but a rotary orientation).
axis, while there is total rotational freedom (the bivector, by its nature, does not identify a direction but a rotary orientation).
Consequently, the representation should be differentiated:
- vectors represent 2D translations, complex numbers 2D rotodilations and should not be confused, on the contrary, this distinction should be taught as soon as possible in high school, for example from the second degree equations.
- the inverse expression does not coincide: for vectors the inverse is given by
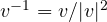 , while for complex numbers we have
, while for complex numbers we have 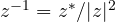 . Conjugation is what differentiates the two expressions and graphically the difference is clearly visible:
. Conjugation is what differentiates the two expressions and graphically the difference is clearly visible:
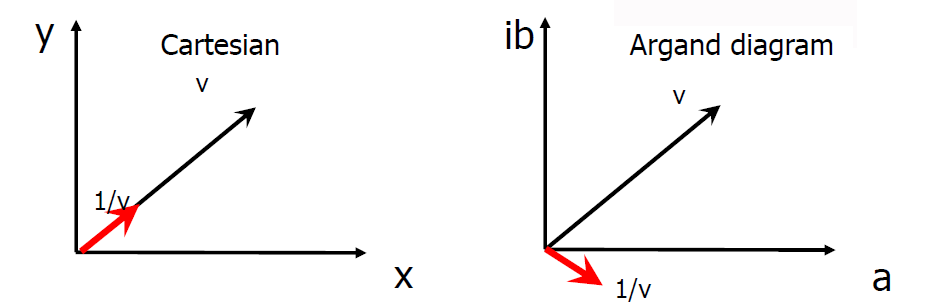
This fact hides a very dangerous pitfall: if we reason on a quantity ![]() represented on the real axis, given that the conjugate coincides with the vector itself, we may never realize that the correct expression to be used in the calculations must predict the conjugate
represented on the real axis, given that the conjugate coincides with the vector itself, we may never realize that the correct expression to be used in the calculations must predict the conjugate ![]() , as in the case of electric power in alternating regime.
, as in the case of electric power in alternating regime.
Having established that vectors and complex numbers are NOT the same thing, despite both operating in two dimensions, it remains to be asked – since they are part of the same algebra – how they can “communicate” these two worlds. In other words, how can we map vectors to complex numbers and vice versa.
As already mentioned, a complex number is a rotodilation operator. We can then see it as an operator that takes the unitary real vector as input and transforms it by rotating and scaling it according to the complex number. The result will be a vector associated with that complex number: ![]() and therefore we can interpret complex numbers as the quotient between a vector and the unit vector:
and therefore we can interpret complex numbers as the quotient between a vector and the unit vector: ![]() that is, that expression that takes the “raw material”
that is, that expression that takes the “raw material” ![]() and maps it throughout the plane.
and maps it throughout the plane.
So if we want to correctly vectorize a complex number, we must multiply it by the vector that we believe to express the real part (say ![]() ):
): ![]() and we will discover that we can construct fractals remaining in a vector space!
and we will discover that we can construct fractals remaining in a vector space!
We close with this table that summarizes similarities and differences between two (indeed three) worlds that are so similar that they can be confused:
| Vectors | Complex numbers | Generalized complex numbers (GA) |
|---|---|---|
| oriented segments in | points in x-iy plane (Argand-Gauss plane) | oriented circle arcs in |
| priviledged axes | priviledged axes | total rotational symmetry |
